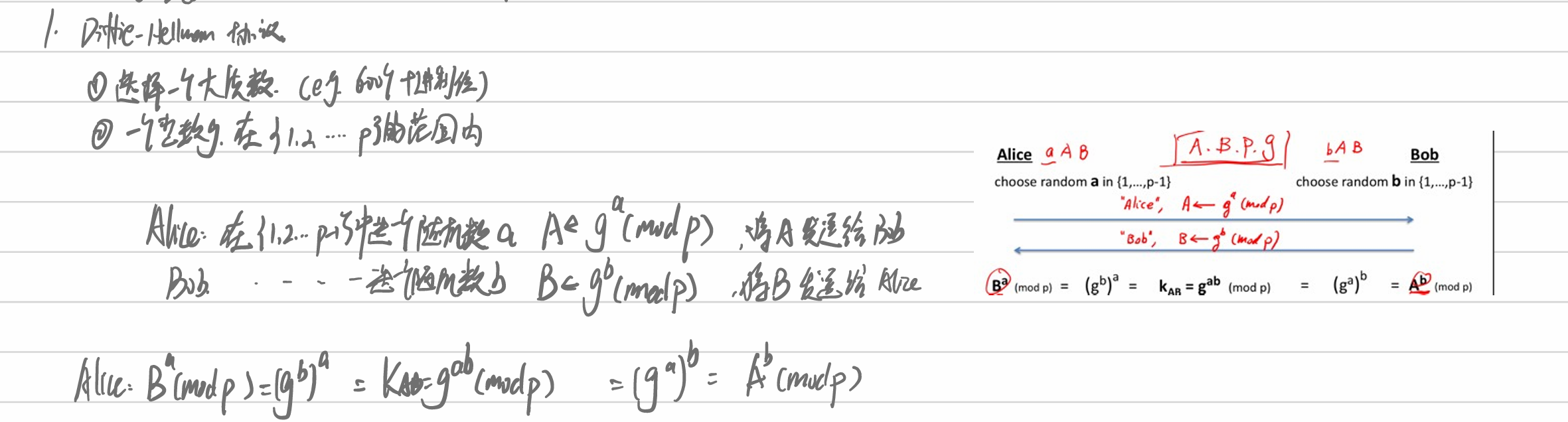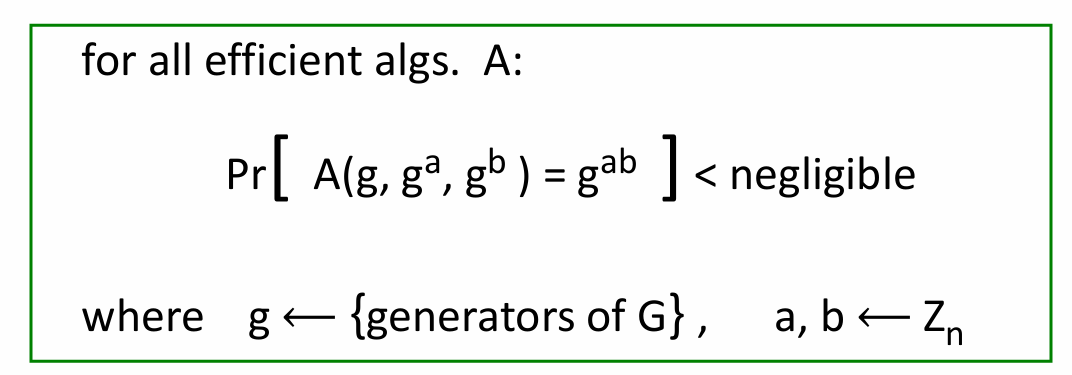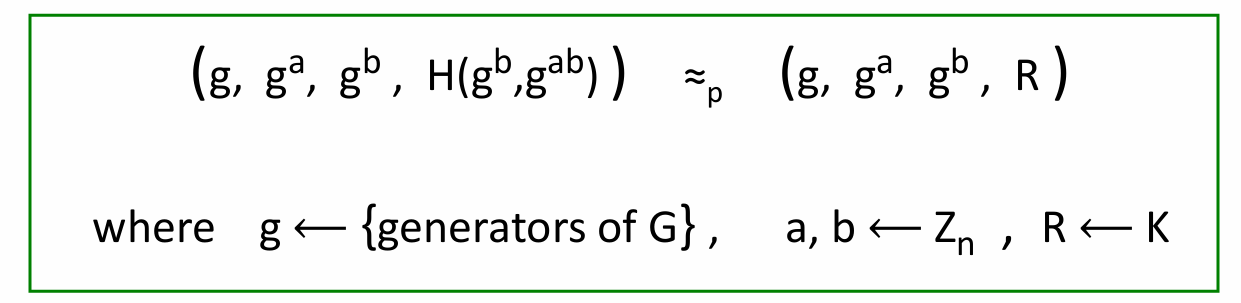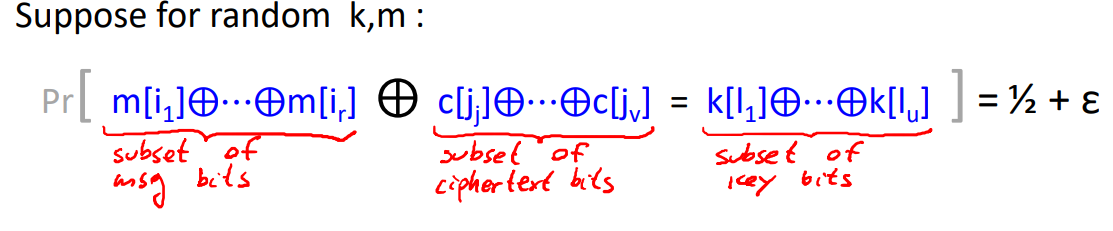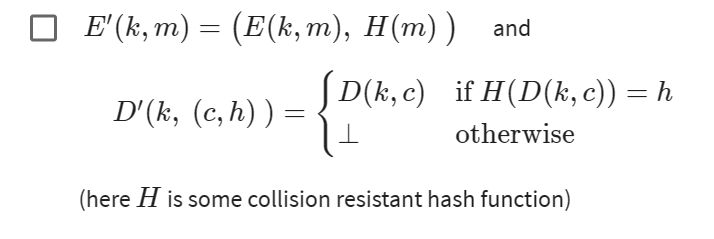信息安全技术
从杂碎开始笔记在概念性的地方的笔记会更简单一些
课程主要内容:
对称加密 公钥加密
消息认证码 数字签名
The joy of cryptography
参考 Dan Boneh
考试:70%考试 30%平时成绩
目的:
- 基本的密码算法及其应用
- 密码算法可证明安全思路
- 学习密码思维方式
- 工程实践中正确运用
GF(P)的生成元;GF(2^m)
二进制加法:进行异或操作即可
乘法:乘上之后模一个不可约多项式
两个困难问题【现代公钥密码技术的安全保障】:大数因数分解(两个很大的素数相乘,很难分解乘法的结果)和离散对数问题
考试
概念性
流密码
-
完美保密性(完美安全性):
任意 任意密文c,同一明文,消息加密后为c的概率相等。
-
PRG
- PRG安全性:定义统计测试算法A(输出0 伪随机,输出1 真随机),一个PRG G,一个真随机r;定义A对G的优势: 如果该优势 是接近1,表明A可以将G与真随机区分,反之接近0 表示不可区分
- PRG性质:
- 安全的PRG是不可预测的;
- 可预测的PRG一定是不安全的;
- PRG G的每一个bit都是不可预测的,则G是一个安全的PRG
-
不可区分:p1和p2不可区分可以说,对于任意有效的统计检测A,有p1,p2两种在{0,1}^n上的分布

-
语义安全性(one-time key)(完美保密性的减弱)
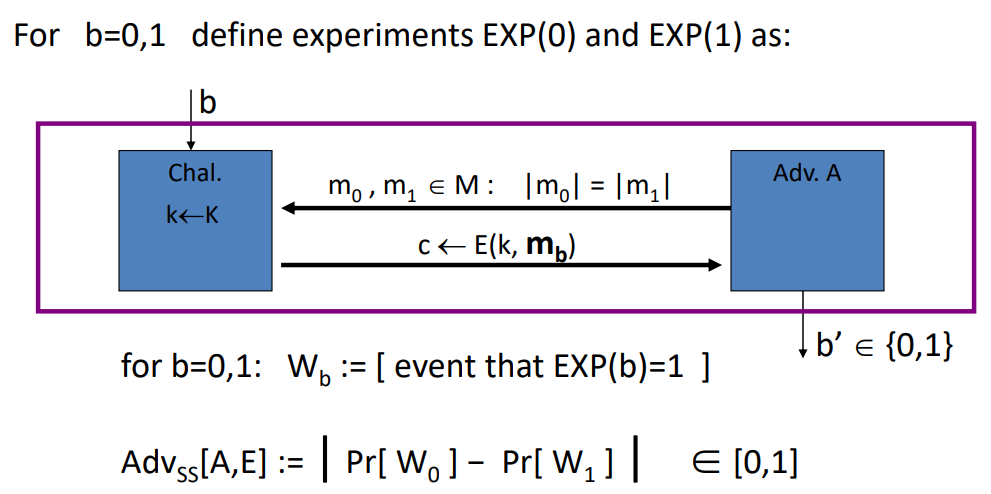
定义了两个实验,优势为在两个实验中输出1的概率的差,如果对所有有效的A语义安全优势 是可忽略的,则称之为语义安全的
- 注意:语义安全性,A只能给挑战者发送一次明文,只能询问一次密文,挑战者的密钥只使用了一次
- 语义安全性例子:可推断LSB的算法A安全性(从输出的角度)、OTP的安全性(从分布的角度)
- 流密码的语义安全性:如果G是一个安全的PRG,则基于G的流密码E是语义安全的。因为:对任意语义安全的对手A,总是存在一个PRG对手B,使得
- 详细证明看笔记
分组密码
-
分组密码性能与流密码性能对比(分组比流密码块):
- 3DES:分组大小64bit 密钥168bit(56*3)
- 3DES轮数:48(3*16)
- 3E((k1,k2,k3),m)=E(k1,D(k2,E(k3,m)))
- k1=k2=k3 3DES会变成single的DES
- AES:分组大小128bit 密钥128,192,256bit
- AES轮数:10
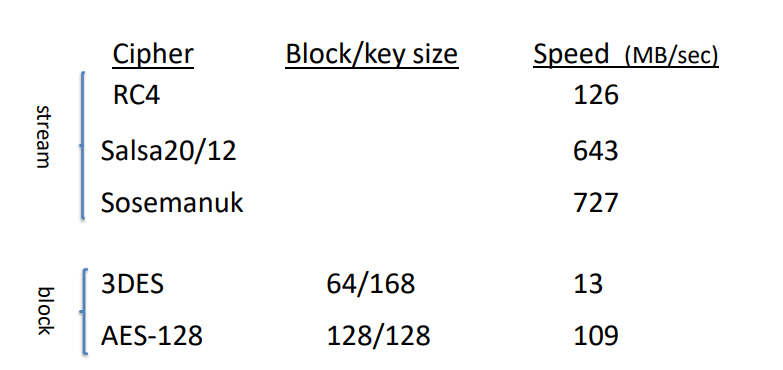
- 3DES:分组大小64bit 密钥168bit(56*3)
-
伪随机函数PRF:F:K*X->Y
-
伪随机置换PRP:E:K*X->X
- 存在确定、有效的算法E(k,x)
- E(k,*)是一对一的
- 存在有效的逆算法 D(k,y)
- PRP是一个输入空间=输出空间的PRF且它可以有效求逆
- AES是PRP(K*X->X;K=X={0,1}128);3DES也是PRP(K*X->X;X={0,1}64,K={0,1}^168)
-
安全的PRF、PRP:
-
从PRF构建PRP:如果F是一个安全的PRF,则将PRF按照不同输入拼接(F(k,1)||F(k,2)…)成为一个PRP,则该PRP是一个安全的PRP
-
DES:key长度:56bits 分组大小:64bit
- 核心Feistel网络(看笔记);如果f是一个安全的PRF,则使用该f构造的3轮Feistel网络是一个安全的PRP( )
- DES是16轮的Feistel网络
- 输入64bits明文,首先进行初始置换
- 进行16轮Feistel网络(将密钥k扩展成16个k,k长度为48bit);其中有
- 64bit名为拆开称为两个32bit,对第一个32bit输入
- 首先将32bit扩展为48bit,与 异或
- 异或得到的结果分成8组,分别输入到S盒中查表,从6位置换为4位
- 4*8=32 将8组输出合并
- 将32bit移位到低位
前半段计算f函数的结果,移位到后半段
- 64bit名为拆开称为两个32bit,对第一个32bit输入
- 进行逆置换
- 输出64位明文
- S盒的选取需要注意:不能有线性函数的输出能以较大比例与S盒的输出重合
- 如果是线性,则很容易通过多个DES推出一个DES
- 如果是线性,则很容易通过多个DES推出一个DES
-
AES:密钥长度:128bit/192bit/256bit 分组长度:128bit
- AES使用代换置换网络(而非Feistel),该网络中每回合所有的位都会变
- AES步骤
- 先构造16字节4*4矩阵(将一个分组变成矩阵)
- 然后将矩阵和密钥异或
- 异或结果输入到轮函数
- 最后一个分组只进行字节代换和行变换,不进行列混淆,最后与密钥异或后输出结果
-
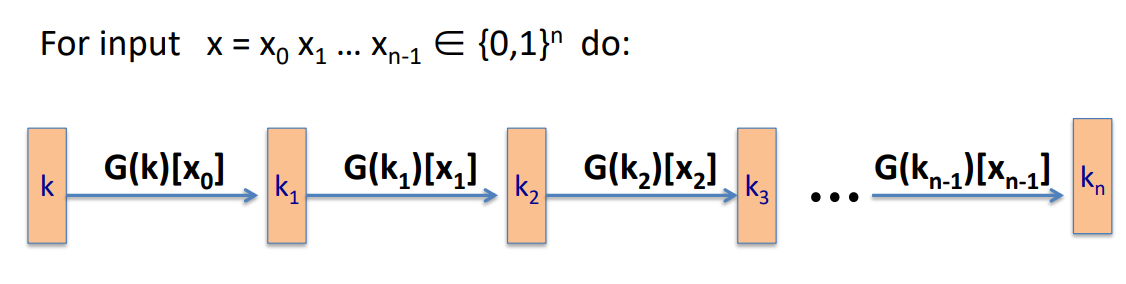
通过PRG构建PRF
-
通过PRF构建PRP?
- 通过GGMPRF 构建一个安全的PRF,然后通过Luby-Rackoff theorem(使用该f构造的3轮Feistel网络)构造出的PRP是一个安全的PRP
-
PRF转换引理:
- 安全的PRP也是安全的PRF,在== |X| 足够大时==
- 引理:对于q次询问的敌手A, A对PRP E的优势与A对PRF E的优势的差的绝对值小于
- 推论:如果 |X|足够大,那么 是可忽略的,则,如果PRP是安全的,即A对PRP E的优势可忽略,可以推出A对PRF E的优势可忽略,因此PRP也是一个安全的 PRF
- 如果X不够大会怎么样?看4.1章节的例题:1bit PRP->PRF
AES应用
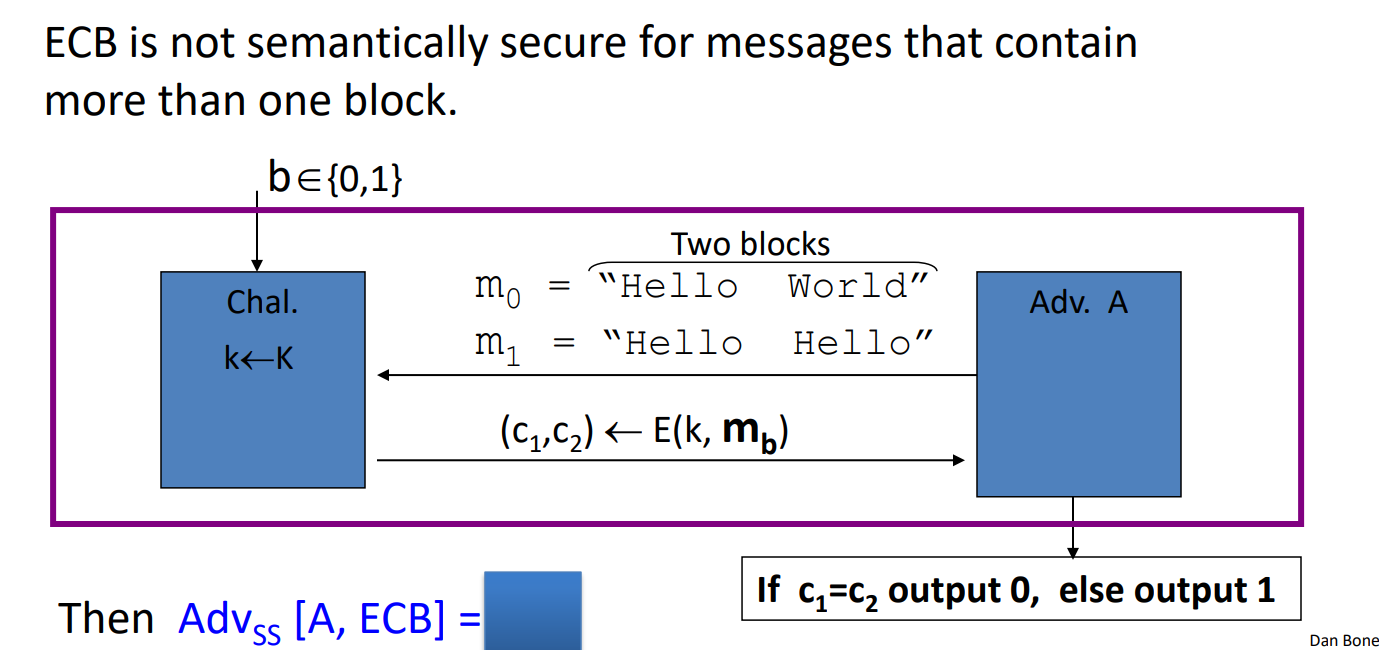
- ECB模式(电码本模式)
- 确定的CTR模式
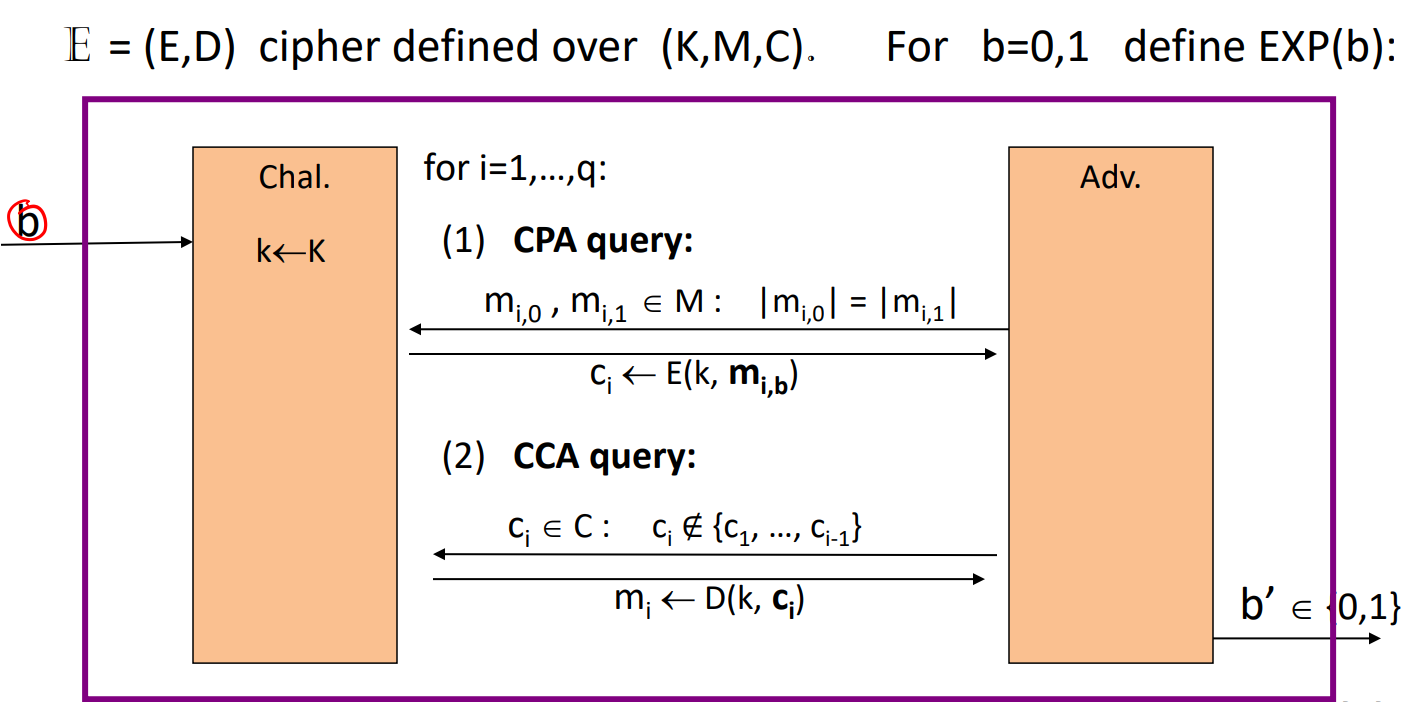
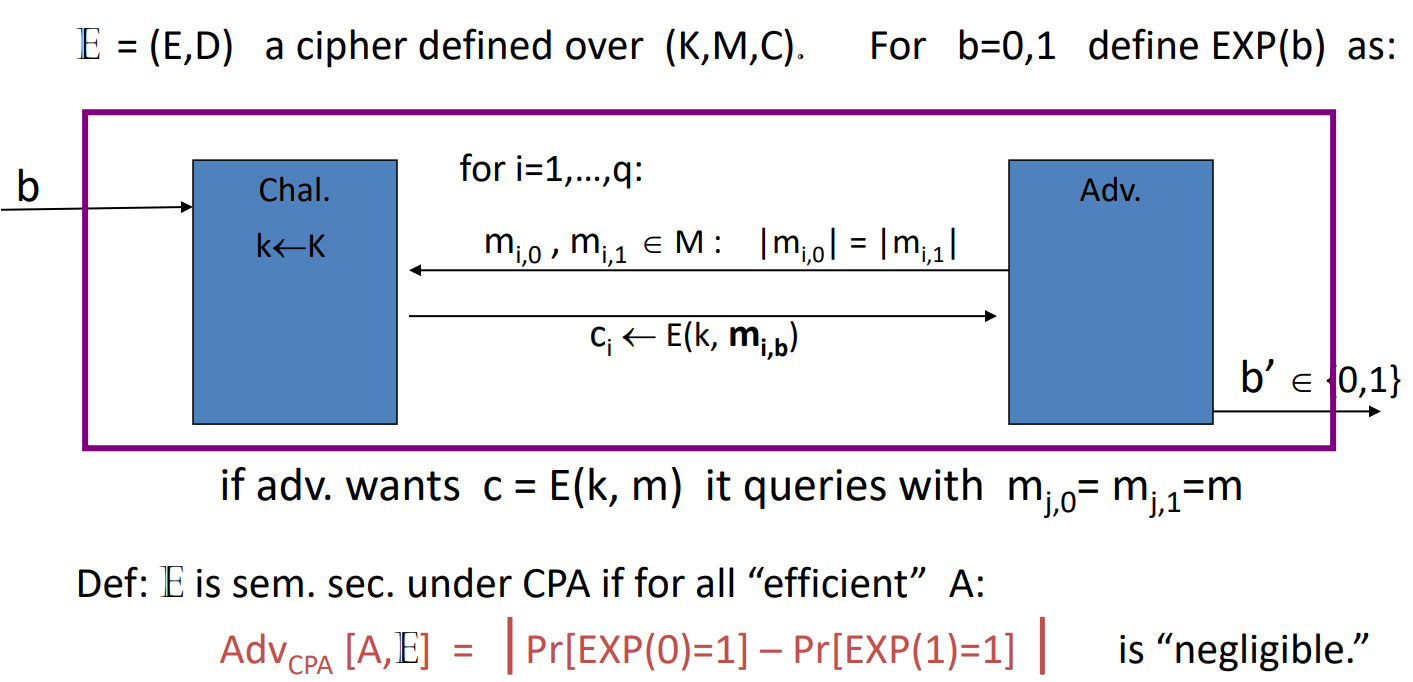
- 多次使用的密钥(Many time Key)下的语义安全性【CPA安全】
- 区别:敌手可以看到多个由同一个key加密得到的消息(此前,一次密钥是只能看到一条用一个密钥加密的消息);选择明文安全:因为敌手可以询问多个明文
- 定义:敌手可以询问q组明文的加密,每次都要猜测挑战者加密的是第一个还是第二个明文
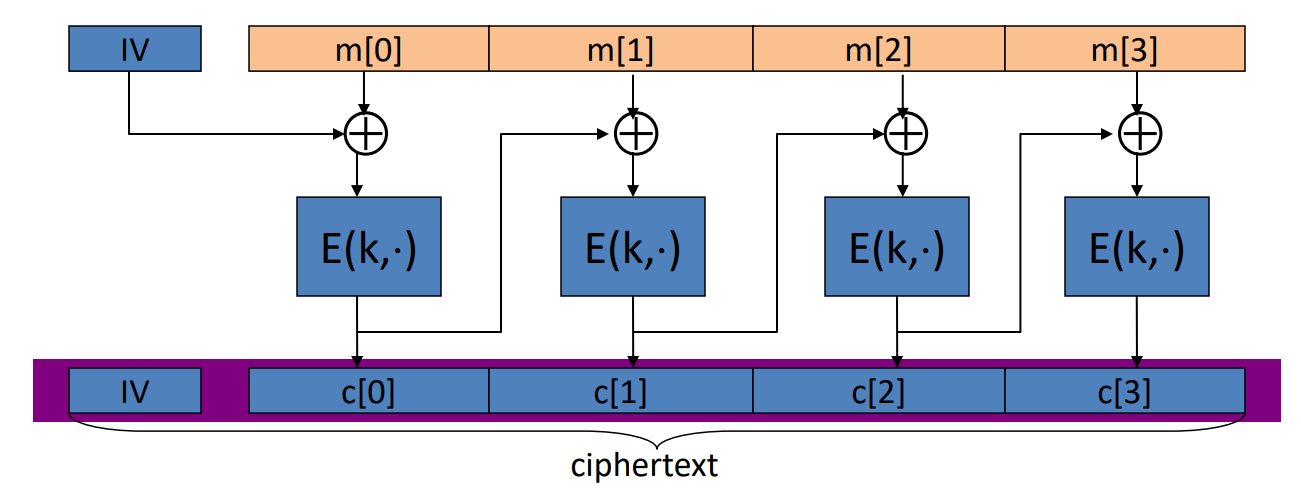
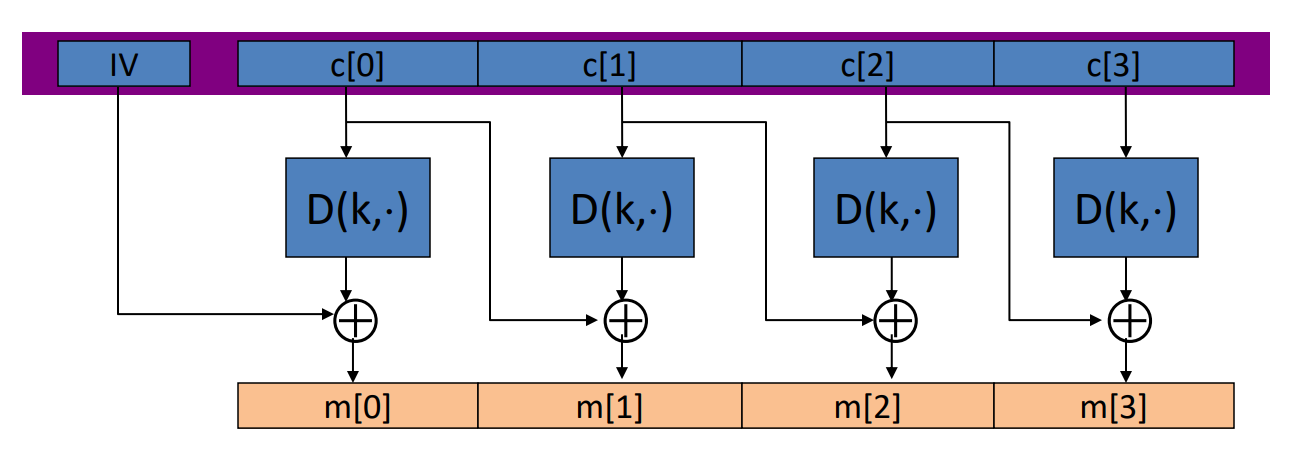
- CBC模式:
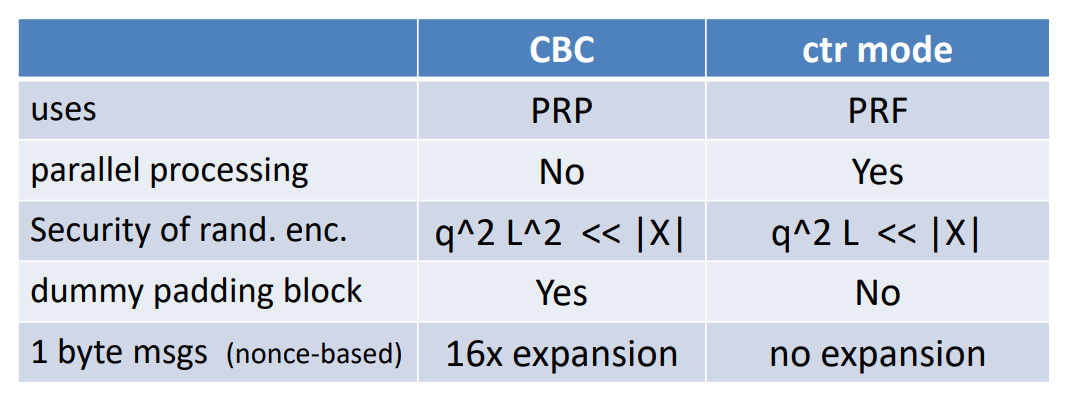
- CTR模式
- 顺序计数器模式:PRF的输入是IV,IV+1…,IV是随机选取的
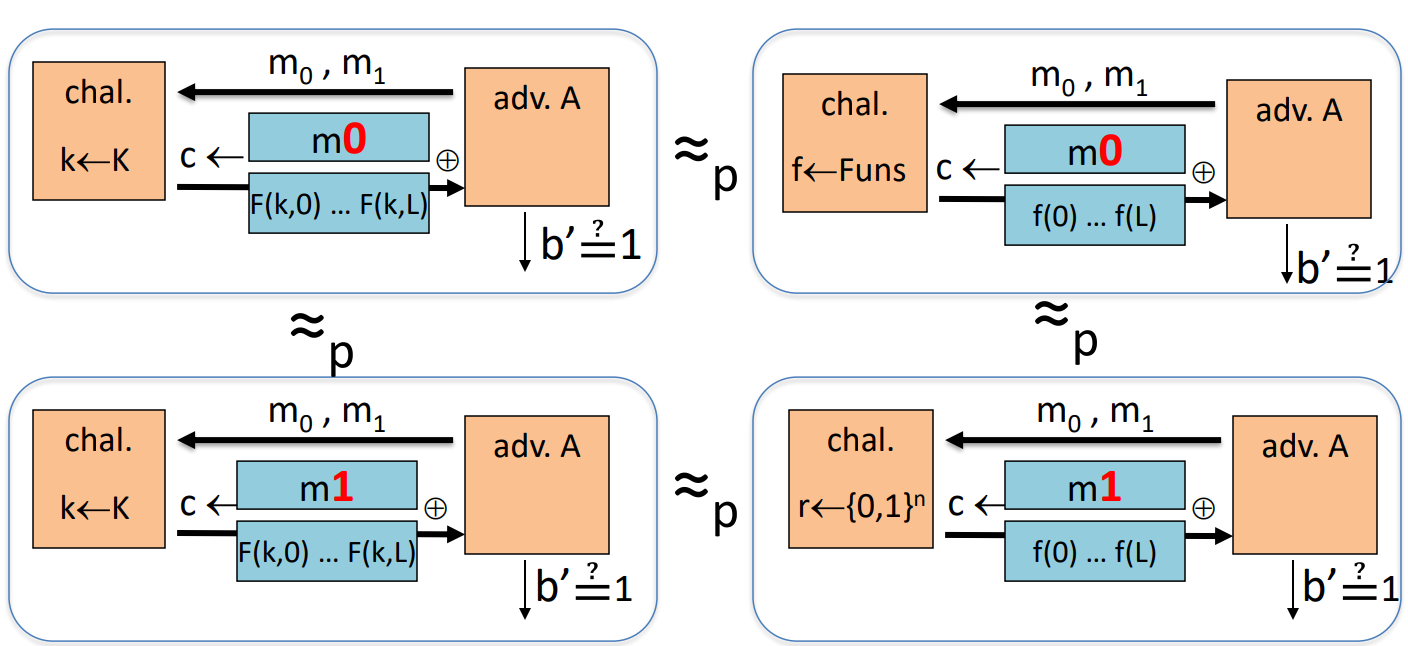
- 计数器模式安全性引理:如果F是一个安全的PRF E是一个CPA语义安全的CTR
只需要 即可满足安全性【比CBC好】
- 计数器模式安全性引理:如果F是一个安全的PRF E是一个CPA语义安全的CTR
- 新鲜值模式:新鲜值不重复,IV=【高位,nonce;低位:计数器】
- 顺序计数器模式:PRF的输入是IV,IV+1…,IV是随机选取的
消息认证码MAC
目的:完整性
- MAC组成:两个算法:S;输出认证tag;V:验证完整性:0/1
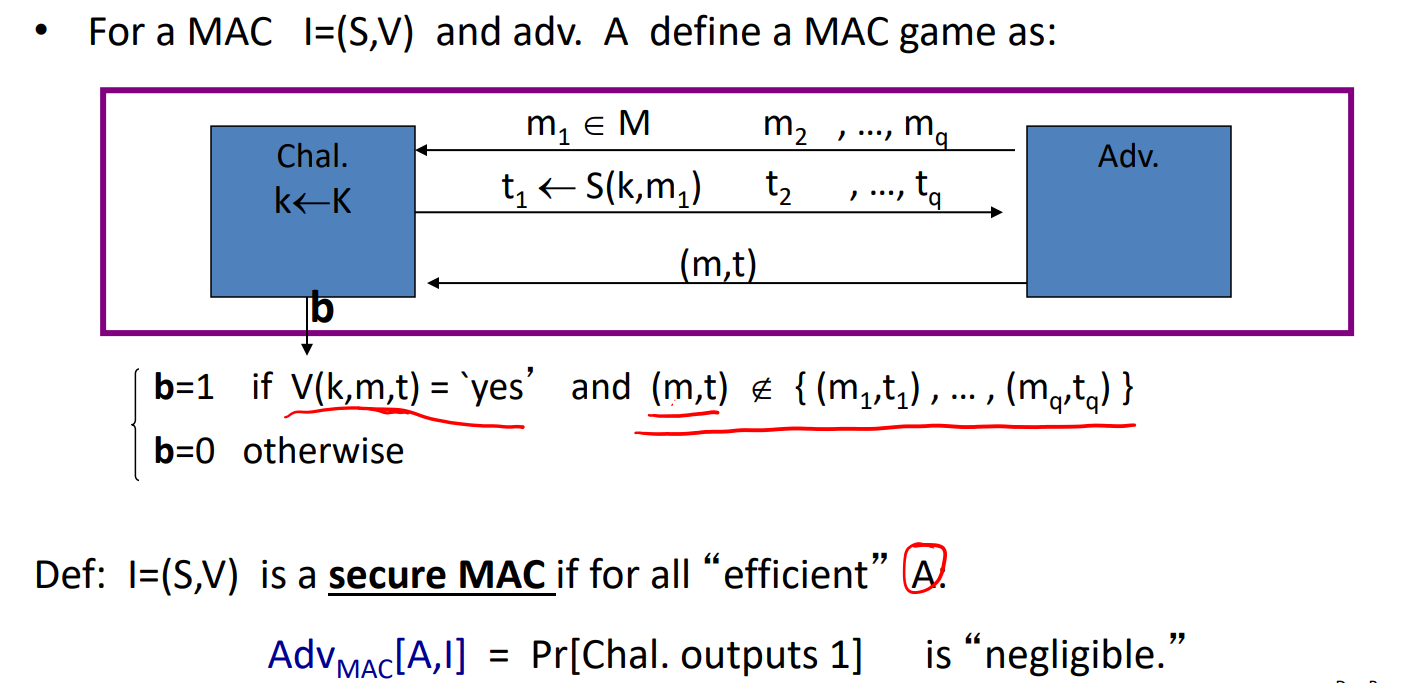
- MAC的安全性:
- 基于PRF的MAC:
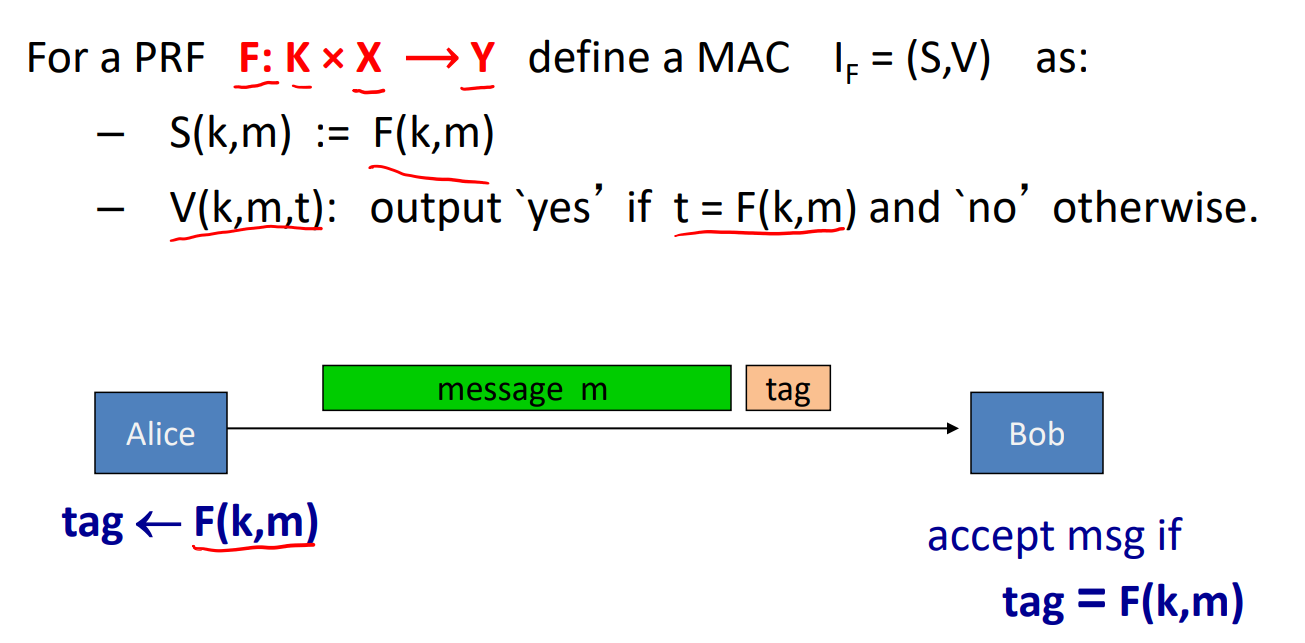
- 安全性计算:如果F是安全的PRF,且F的输出空间 |Y| 足够大,则由此PRF构造的MAC是安全的MAC
- 存在一个对于MAC的敌手A,且存在一个PRF敌手B,使得
- 证明(看笔记)
- 存在一个对于MAC的敌手A,且存在一个PRF敌手B,使得
- 截断基于PRF的MAC:如果有一个安全的PRF构成的MAC是安全的,输出n位,那么截断的MAC,输出w位也是安全的【当且仅当 1/2^w是可忽略的】
- PRF的输入对于一个长消息来说还是太短了,需要CBC-MAC和NMAC
- 安全性计算:如果F是安全的PRF,且F的输出空间 |Y| 足够大,则由此PRF构造的MAC是安全的MAC
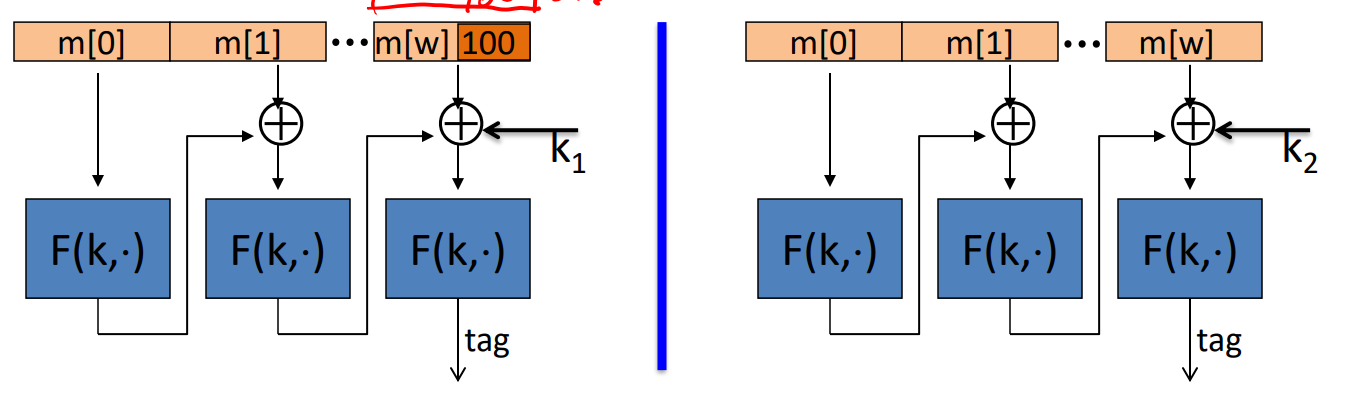
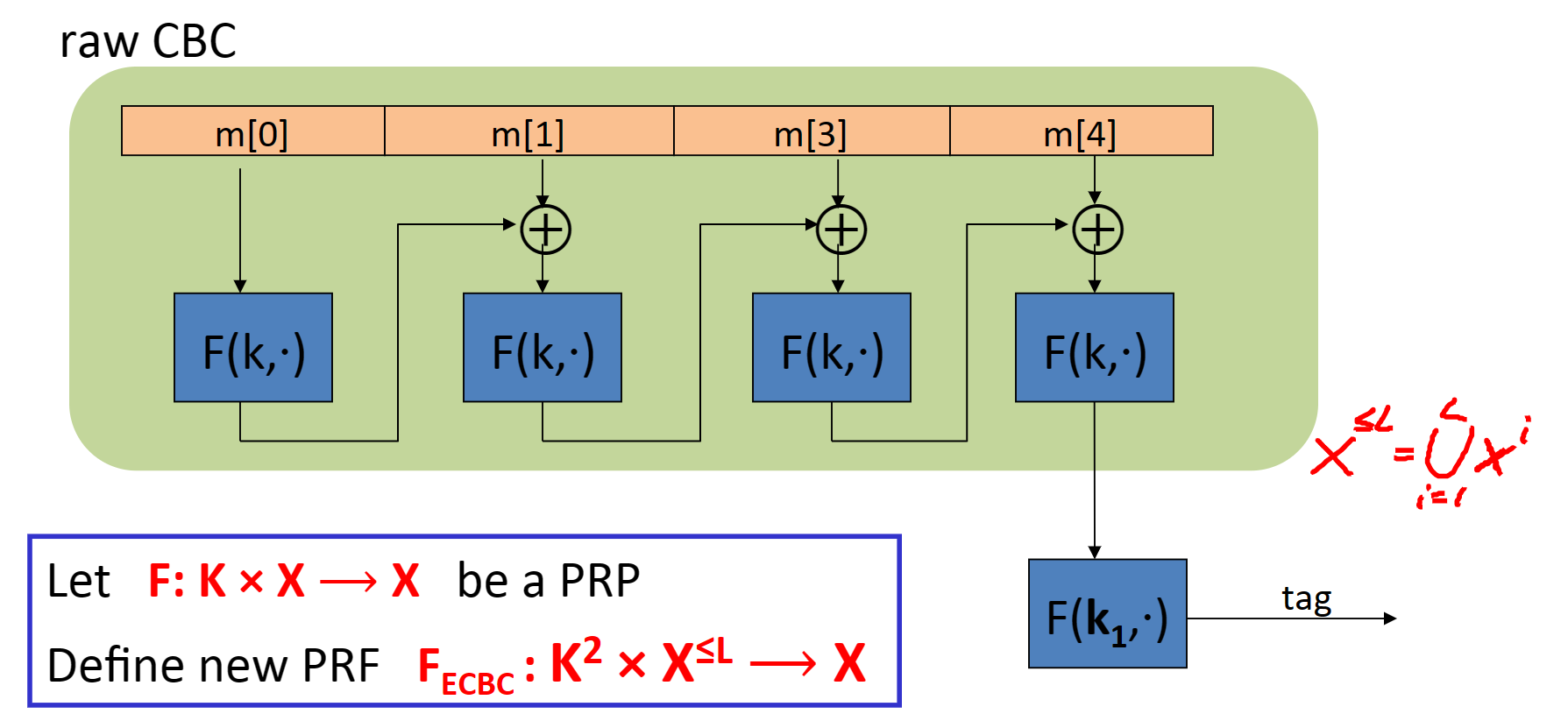
- ECBC-MAC
- 需要两个key
- 通过PRP定义一个新的PRF:
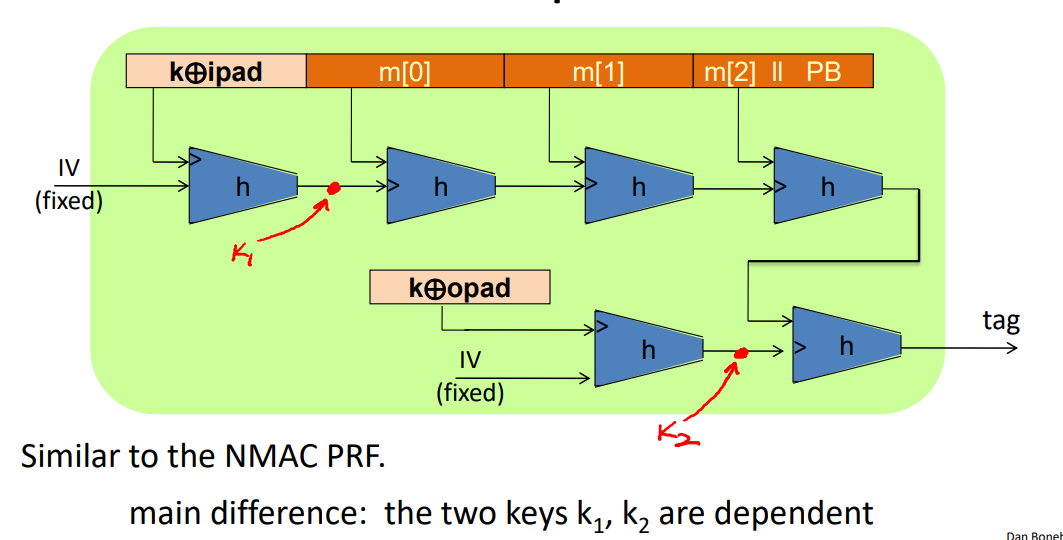
- NMAC
- 也需要两个key 通过级联函数实现
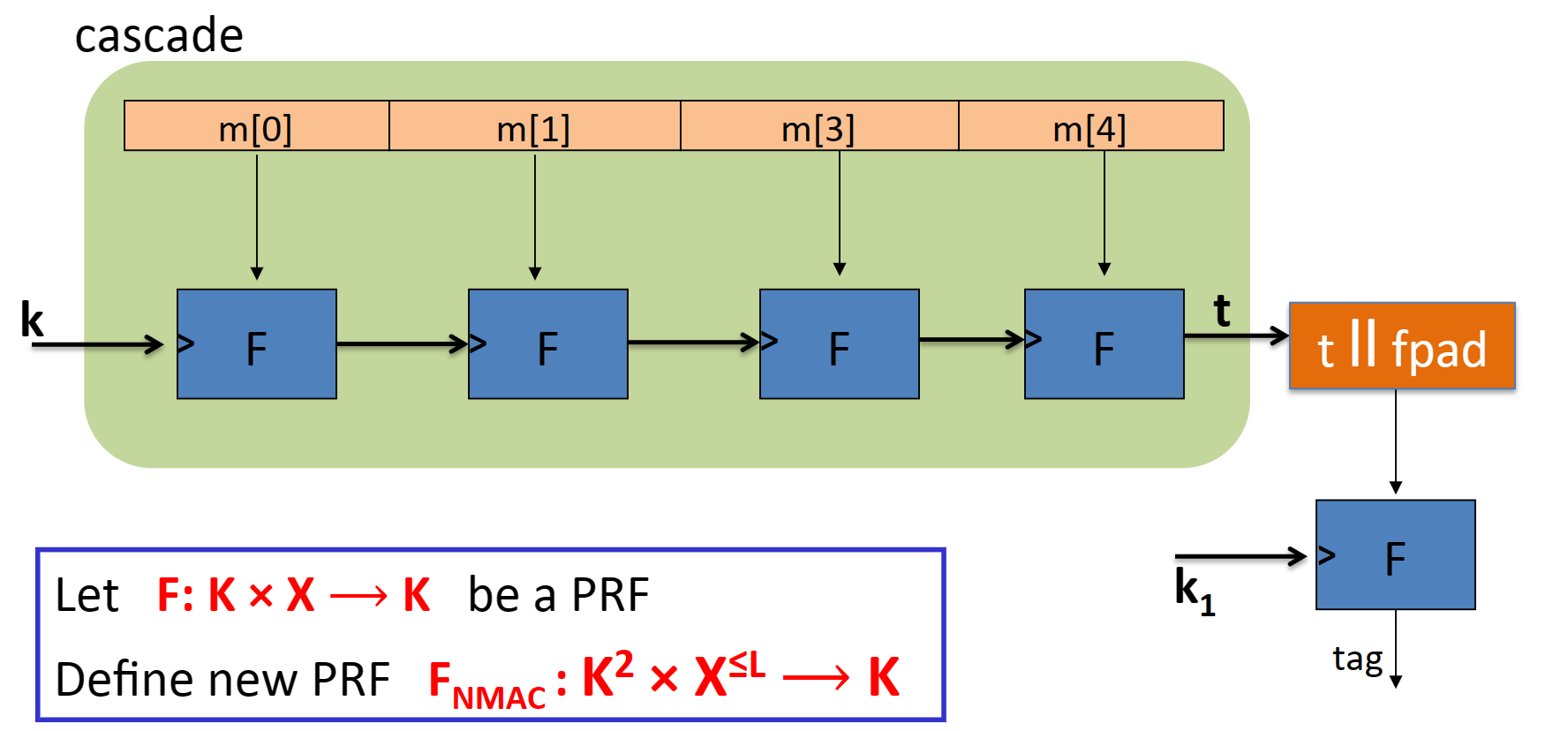
- 如果没有最后一步…会被选择明文攻击攻破【攻击者选一个消息为分组大小n的消息,获取其tag,再将这个消息变成n+1,那么可知最后一个分组与输入F的t,可以成功伪造t;具体看笔记】
- 当 时,CBC-MAC安全
- 随机化的RCBC
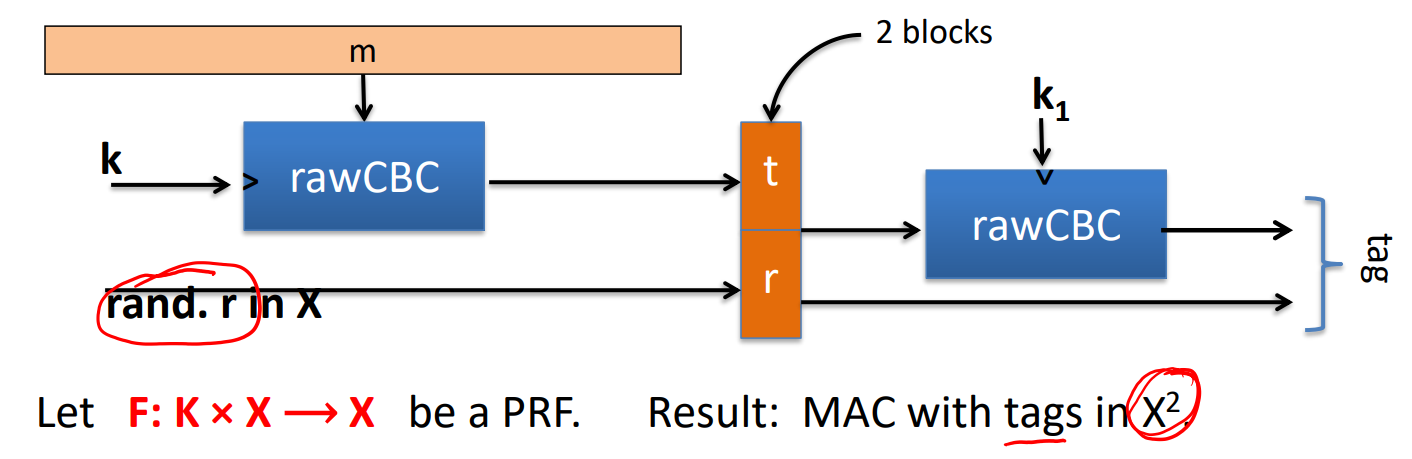
- 安全性:
- CBC MAC的填充:
- PMAC:
- 最后一个分组不加密,需要两个 key
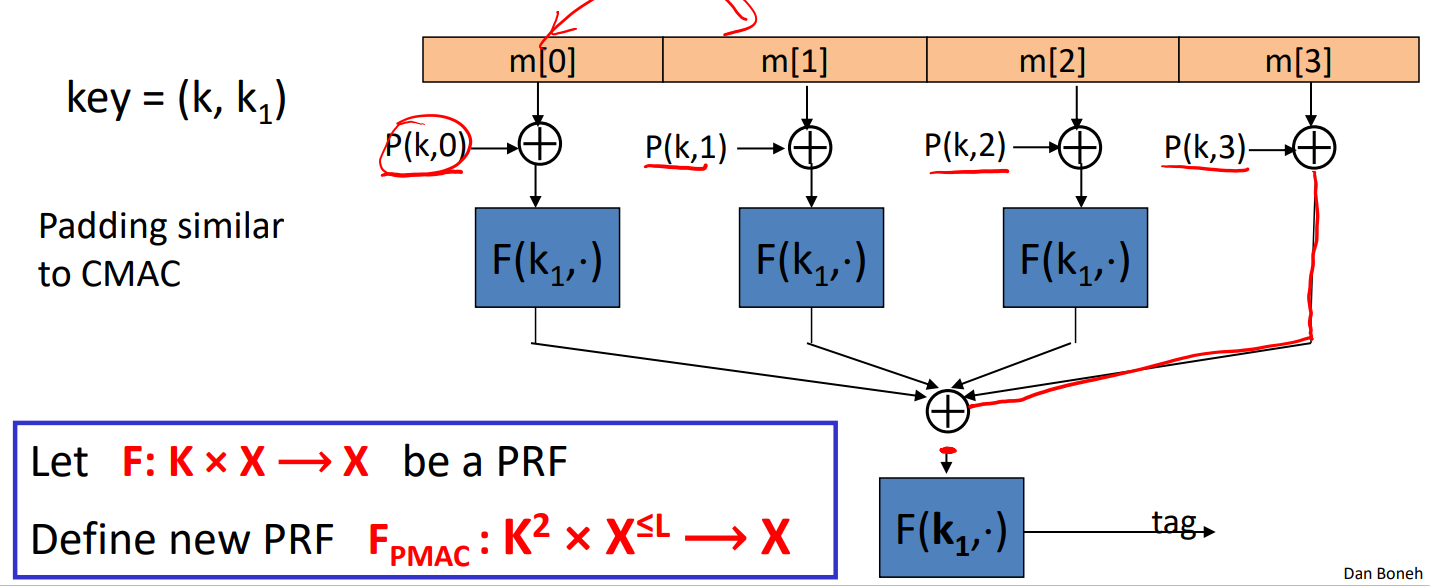
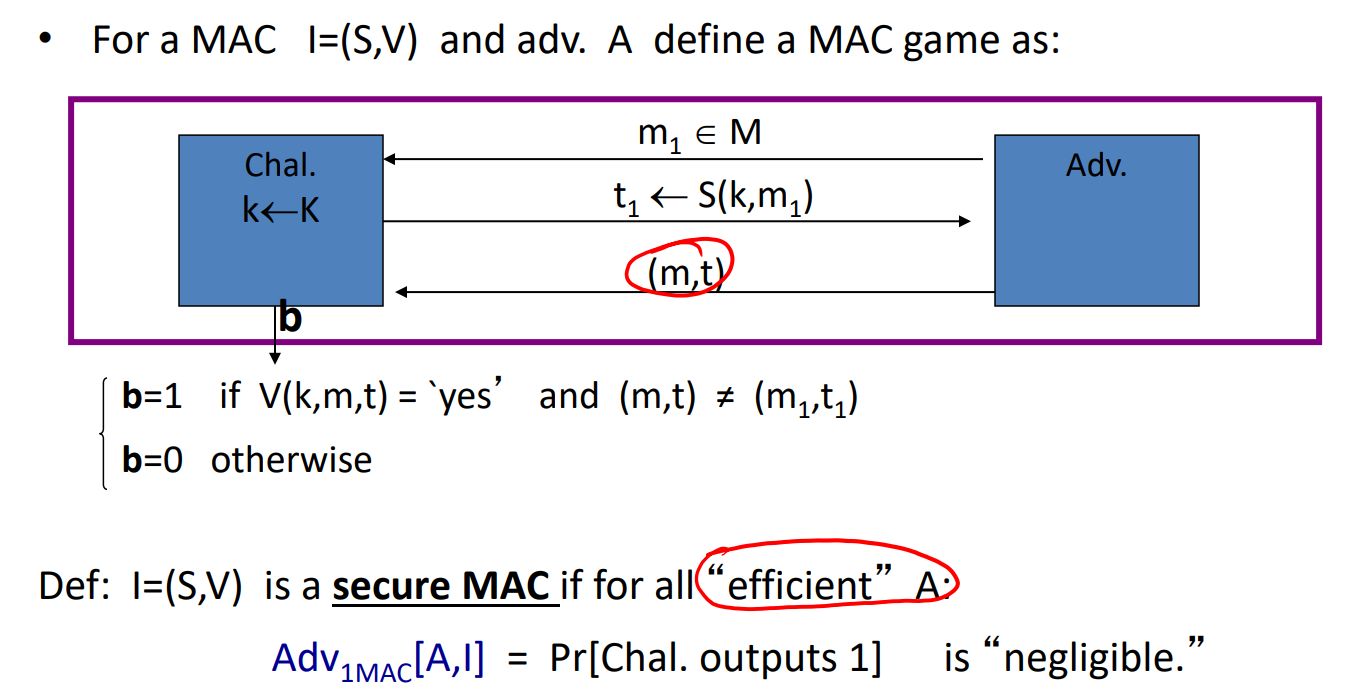
- 一次性MAC
- 一次性MAC->many-time MAC
- 使用one time MAC构造可快速求得的many-time MAC
- Carter-Wegman MAC: ;其中,F是一个安全的PRF,S是一个oneTime MAC,r是一个随机值
- 总结

哈希函数
- 生日悖论:

- 哈希函数
- H:M->T 是一个哈希函数(|M|>>|T|,大空间到小空间)
- 碰撞:m0!=m1,H(m0)=H(m1)
- 哈希函数的抗碰撞:对任意有效算法A, 是可忽略的
- 通过抗碰撞构造MAC
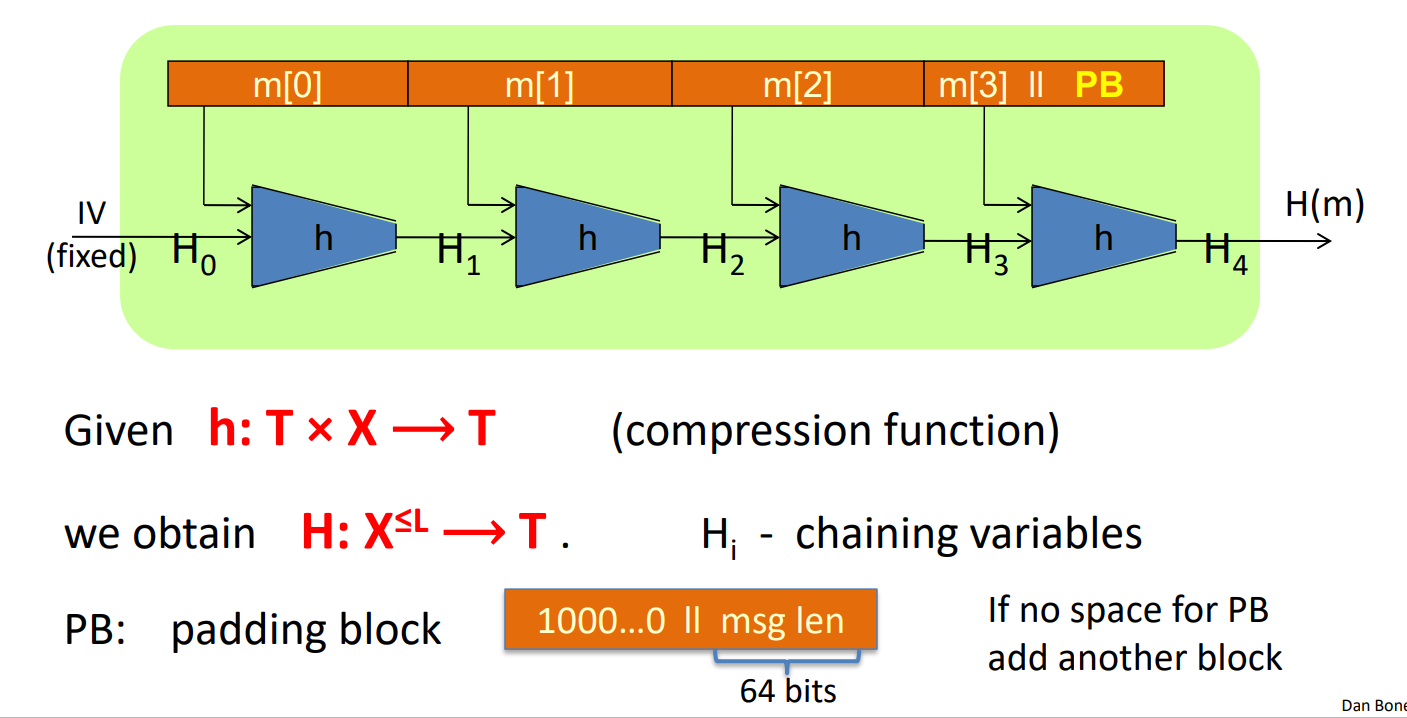
- Merkle-Damgard
- 构建安全的压缩函数
- 从分组密码制造压缩函数
- Davies-Meyer压缩函数:
- 从分组密码构造压缩函数
- Miyaguchi-Preneel: 以及
- 不安全的:
- 从分组密码制造压缩函数
- 从难解问题构造压缩函数:利用离散对数问题,但是很慢

- HMAC(从SHA-256)
认证加密
- 认证加密是为了防止篡改攻击【提供保密性和完整性】,实现了选择密文攻击的安全性,认证加密可以推出CCA安全
- 认证加密:认证加密系统 (E,D)
- 为了安全性,必须提供:CPA攻击下的语义安全;密文完整性(攻击者不能构造一个可被正确解密的密文)
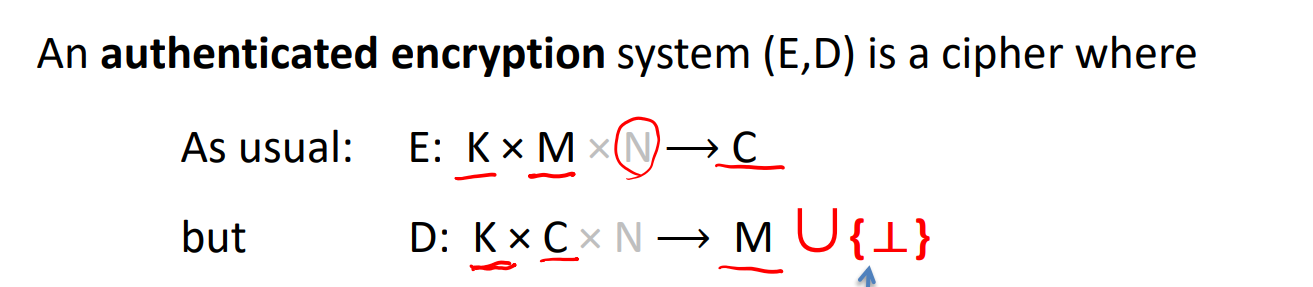
- 密文完整性 CI 的定义与认证加密的定义
- 选择密文攻击安全 CCA安全
- 认证加密定理:如果(E,D)是CPA安全的加密,(S,V)是安全的MAC,则先E后M总是安全的;先M后E可能对CCA不安全,但是如果加密算法是随机CTR(一次MAC)或者随机CBC,那么先M后C是安全的
- 注意,MAC必须要是安全的,不然攻击者会找到碰撞,导致获得一个密文后,总是能构造出正确解出的明文(例子看笔记)
- OCB:直接从PRP构造的认证加密;高效可并行【有省略】
杂项
- 密钥获取:一般来说会通过一个SK(从硬件随机数发生器或密钥交换协议生成)去通过密钥生成函数(KDF)获取多个密钥
- 密钥推到函数KDF:
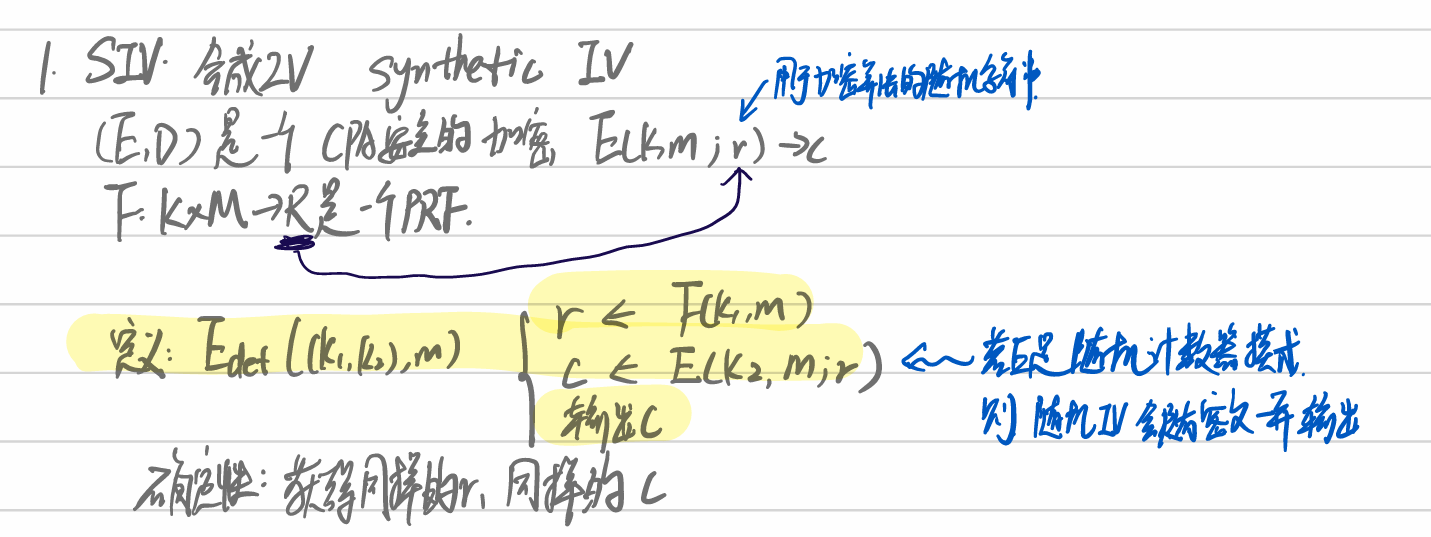
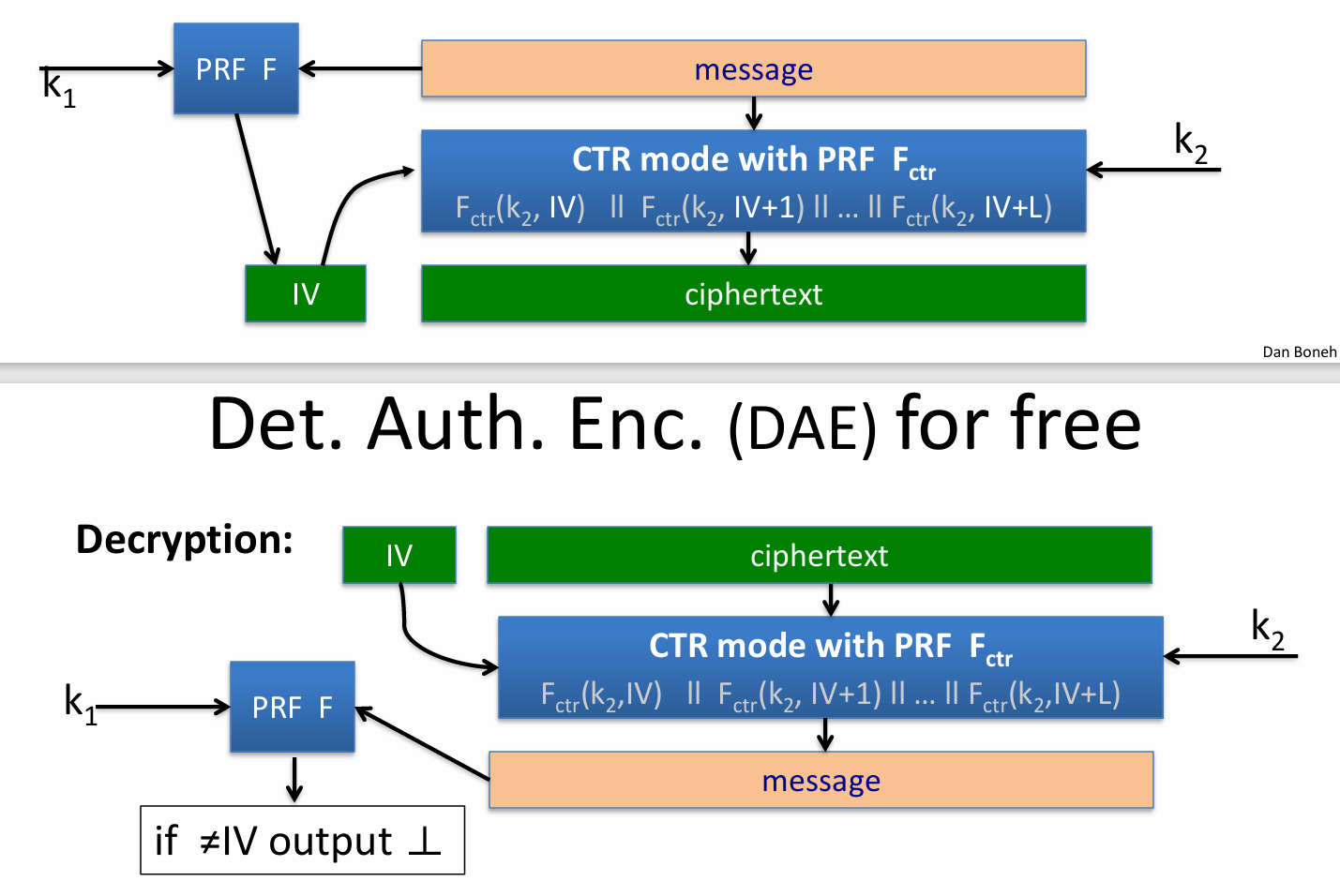
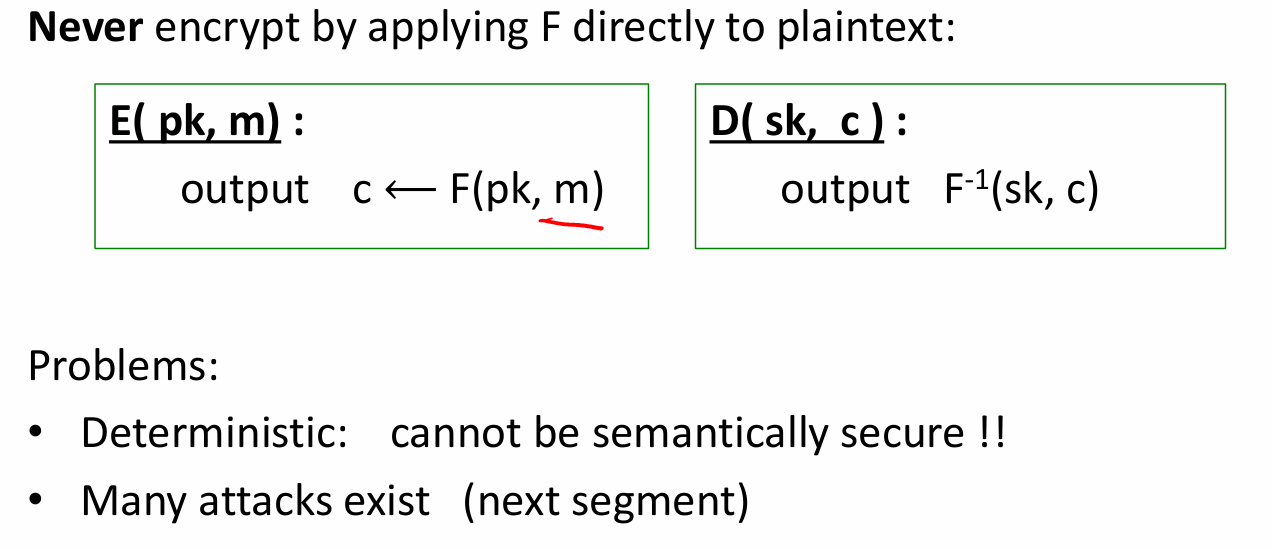
- 确定性加密:概念
- 构造确定性加密
密钥交换
- key的管理:每个人各自存一个密钥,每个人需要O(n)个密钥;使用信任的第三方(TTP),每个人只需要一个key
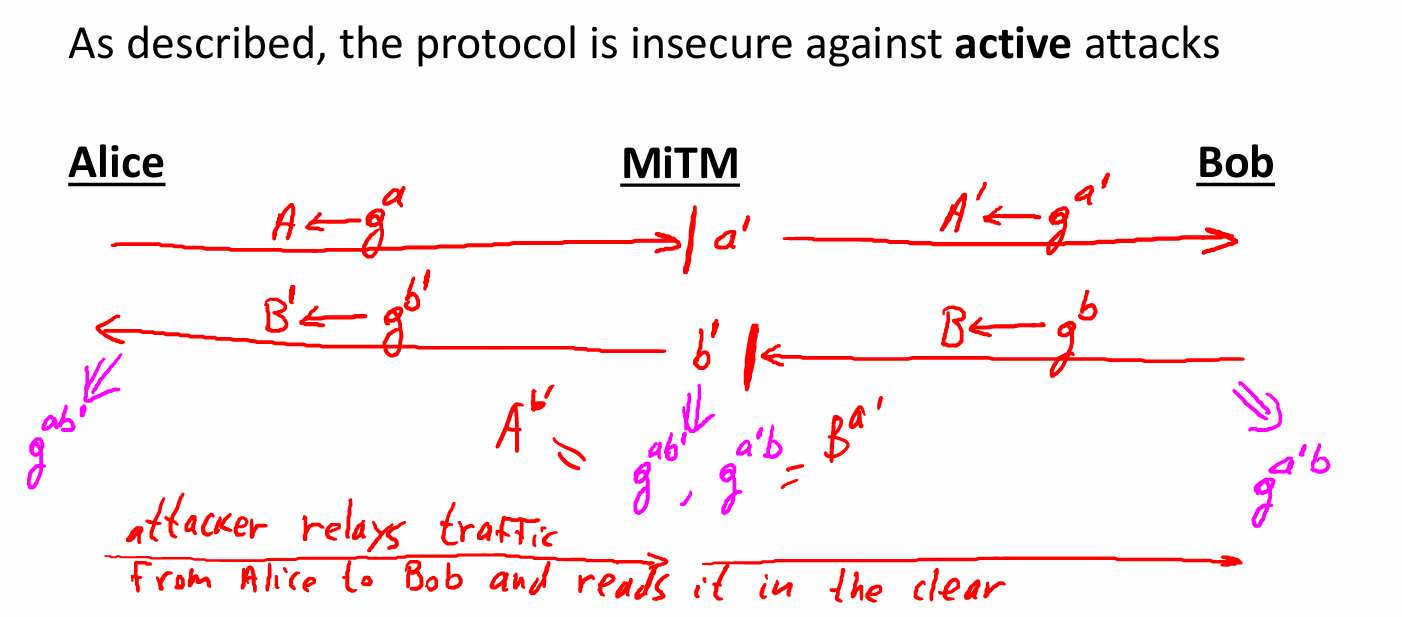
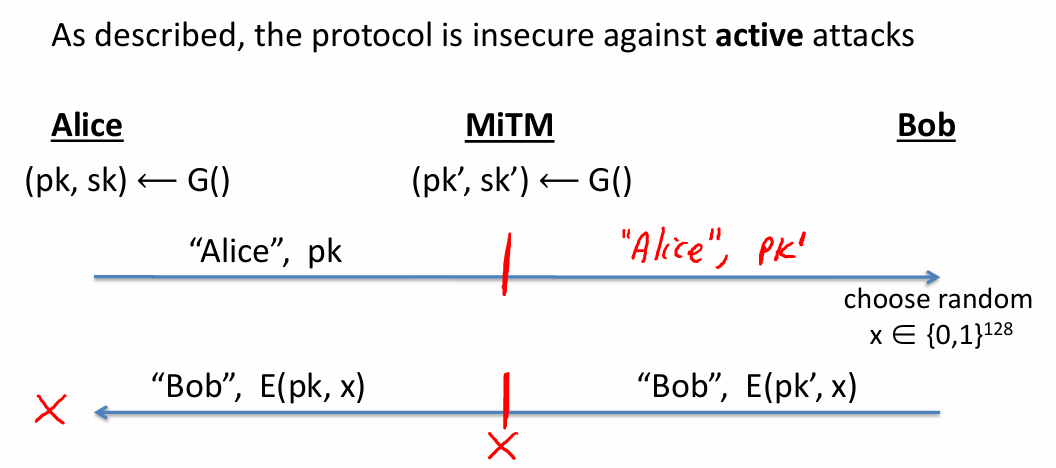
- 密钥生成的玩具协议:抵抗窃听攻击但是不抵抗篡改攻击
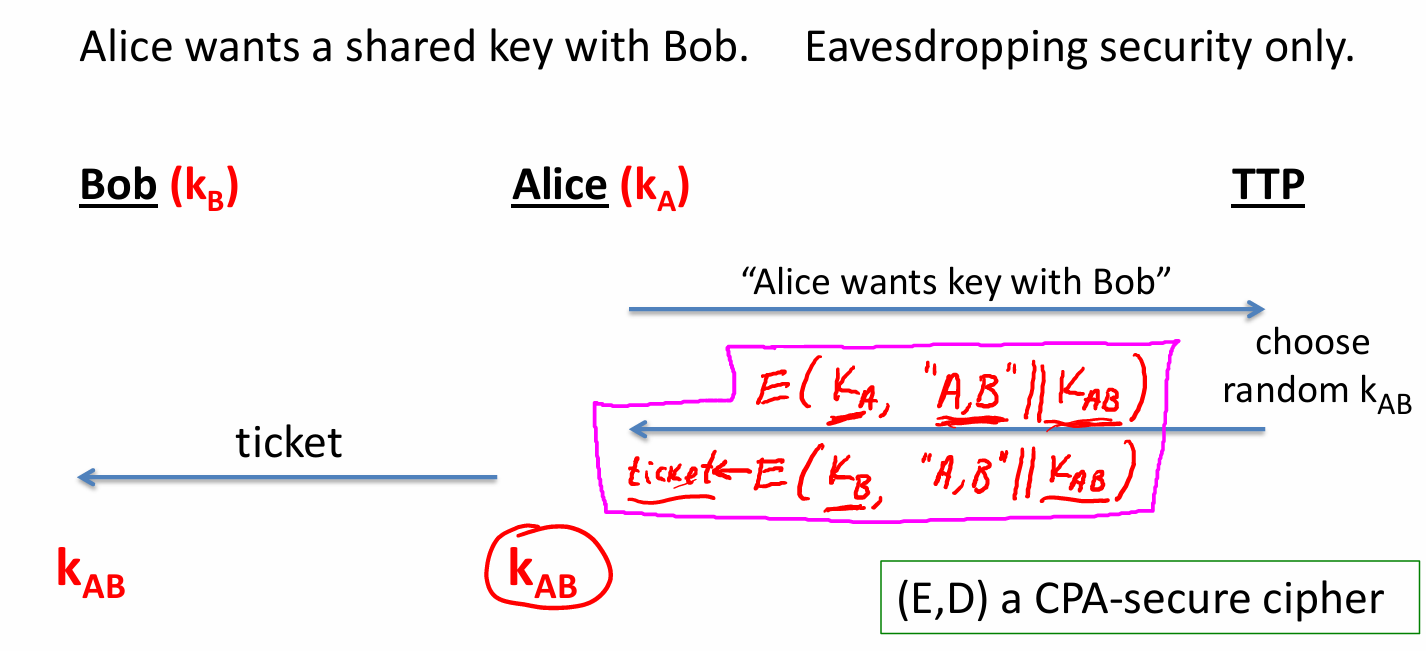
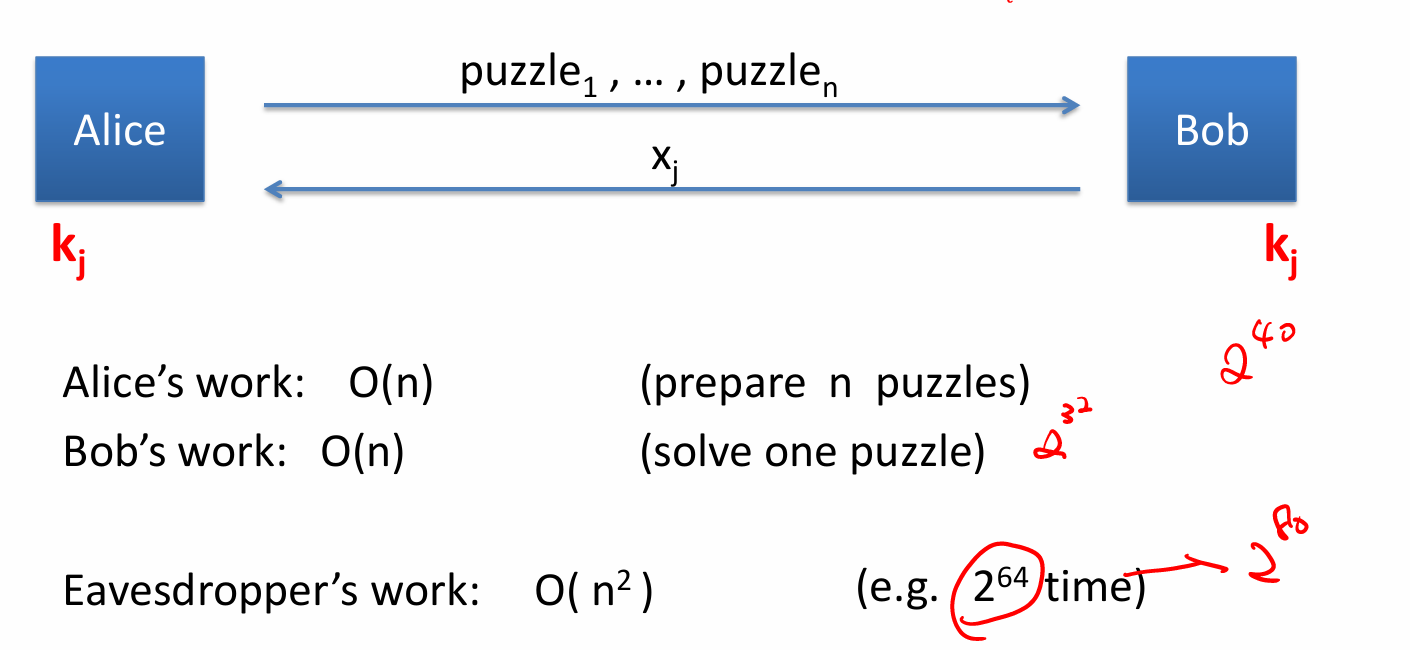
- Merkle Puzzle
- Diffie-Hellman 协议
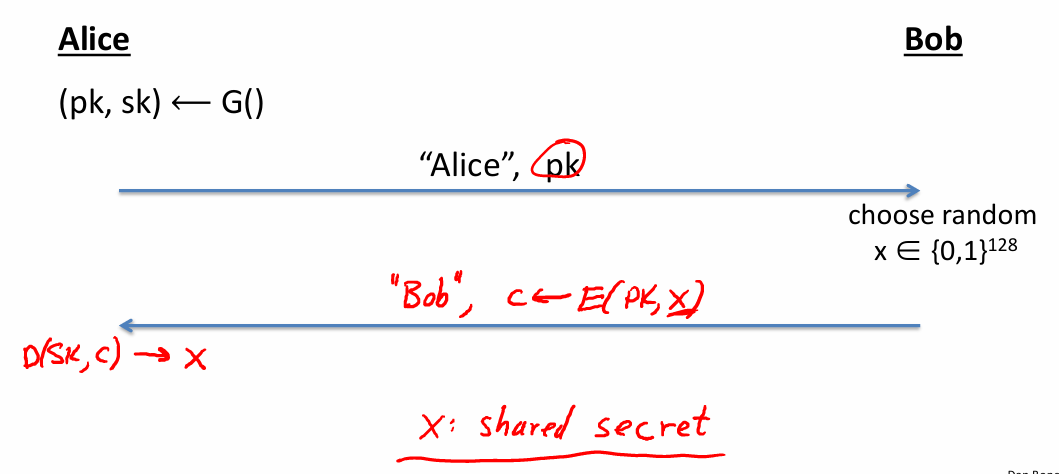
- 建立共享私钥
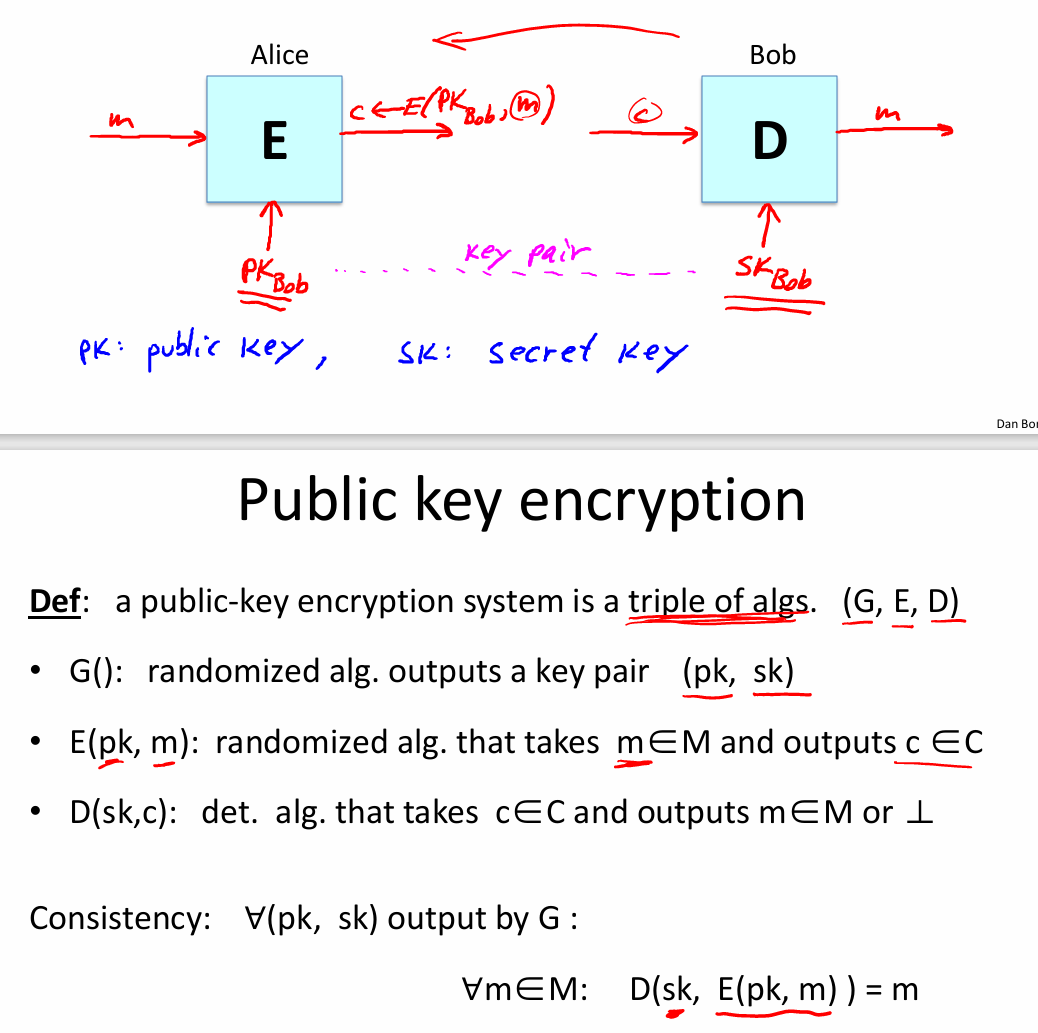
公钥加密RSA
上课透了::::注意公钥加密的CPA安全性的定义
mark:我想思考,公钥加密的CPA安全和普通CPA安全的区别?几个典型的攻击?
对称加密:有one-time 安全和 many-time安全(CPA);一次密钥安全和CPA安全之间是不同的,一次密钥安全不能推出CPA安全
公钥加密:一次安全可以推出CPA安全,这是因为攻击者知道pk之后就可以自己随意加密msg,这和CPA安全是一样的
公钥加密来说,G一定是随机的
- 公钥加密的CPA安全(看上一章节的最后一节)
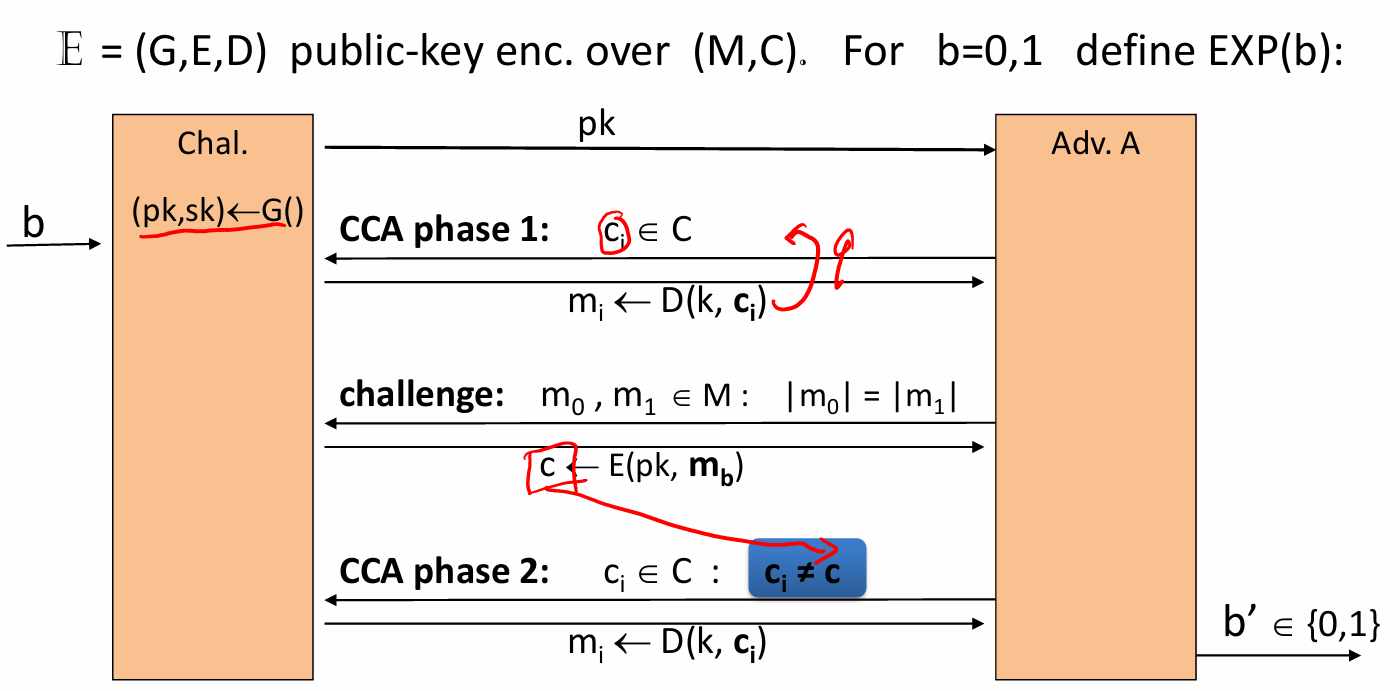
- 公钥加密的CCA安全
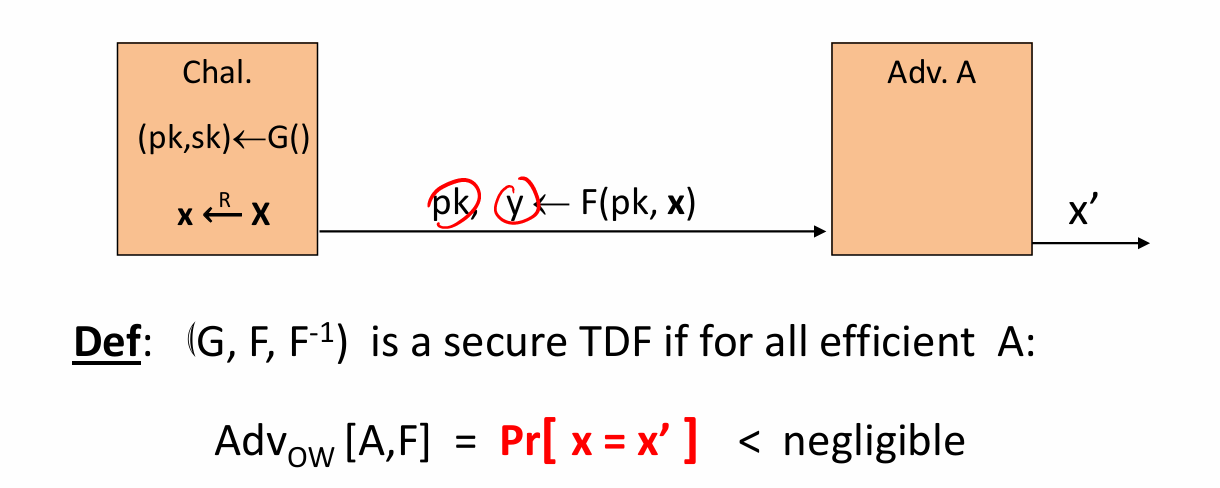
- 陷门函数
- RSA陷门置换函数
- RSA是单向函数:
RSA问题:已知e^x(mod N) 求x;该问题的求解只能将N进行因子分解,但是因子分解是一个难解问题,因此RSA是一个单向函数- RSA最小的指数为3,即最小的e为3
- 错误提高RSA性能:不能使用小私钥来加快解密,使得指数计算缩短来让==>这样会导致私钥可以通过(N,e)计算
- RSA的应用
- 可以使用较小的e加速RSA解密,e最小是3,一般推荐2^16+1
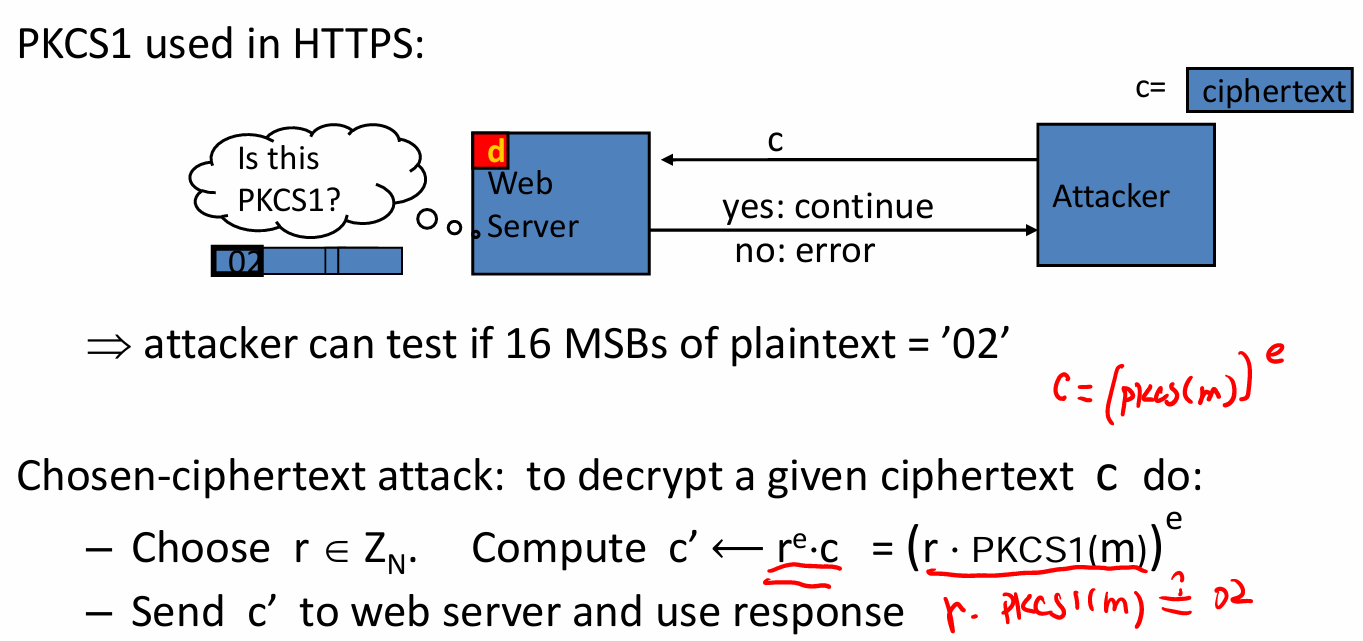
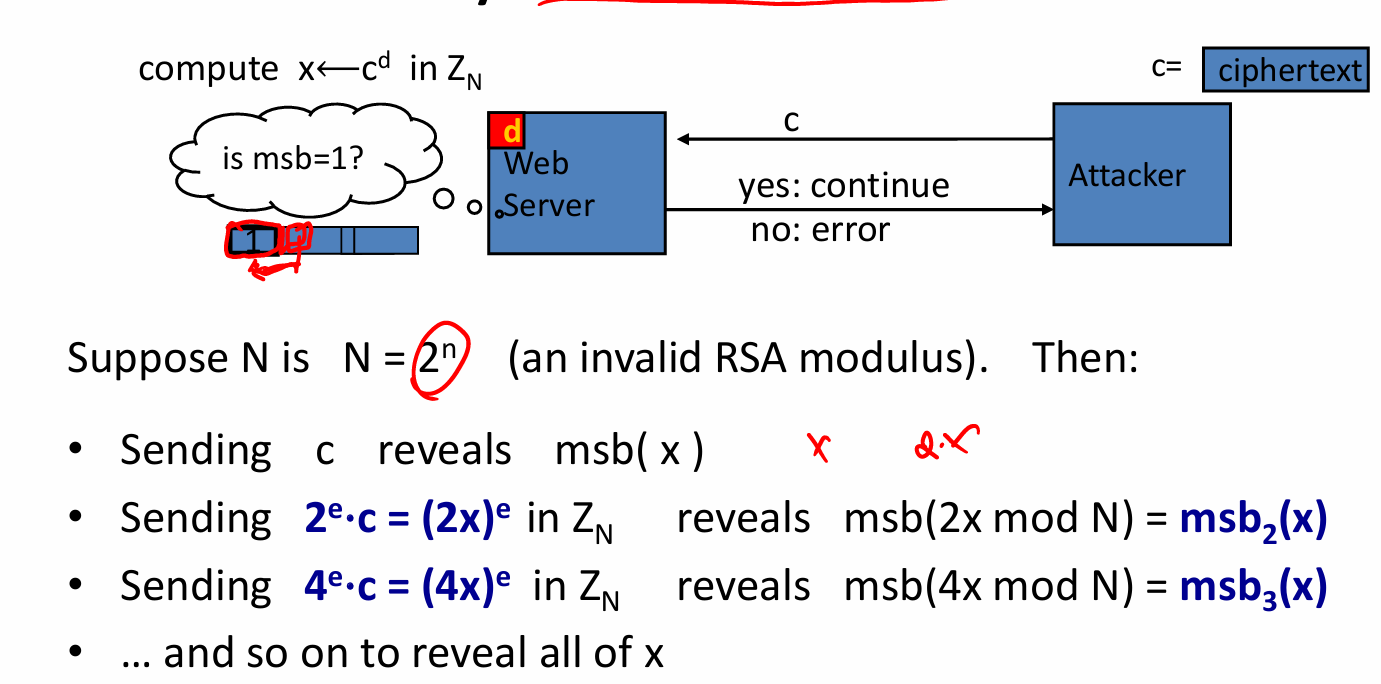
- 针对RSA的攻击(见后面)
公钥加密ElGamal
-
Elgamal:将DH协议转换为公钥加密
- 密钥交换:
- 作为公钥; 通过 计算出k然后解密
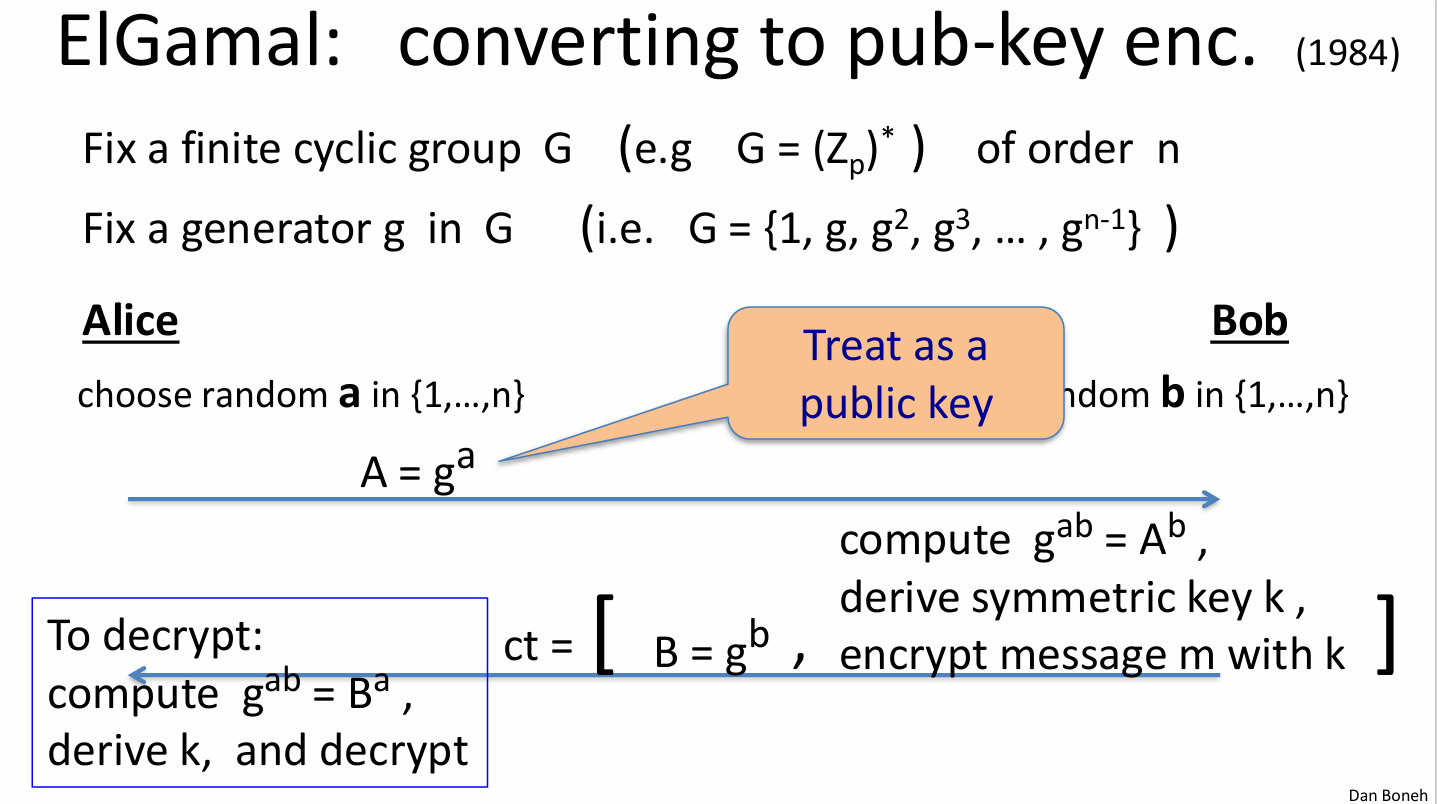
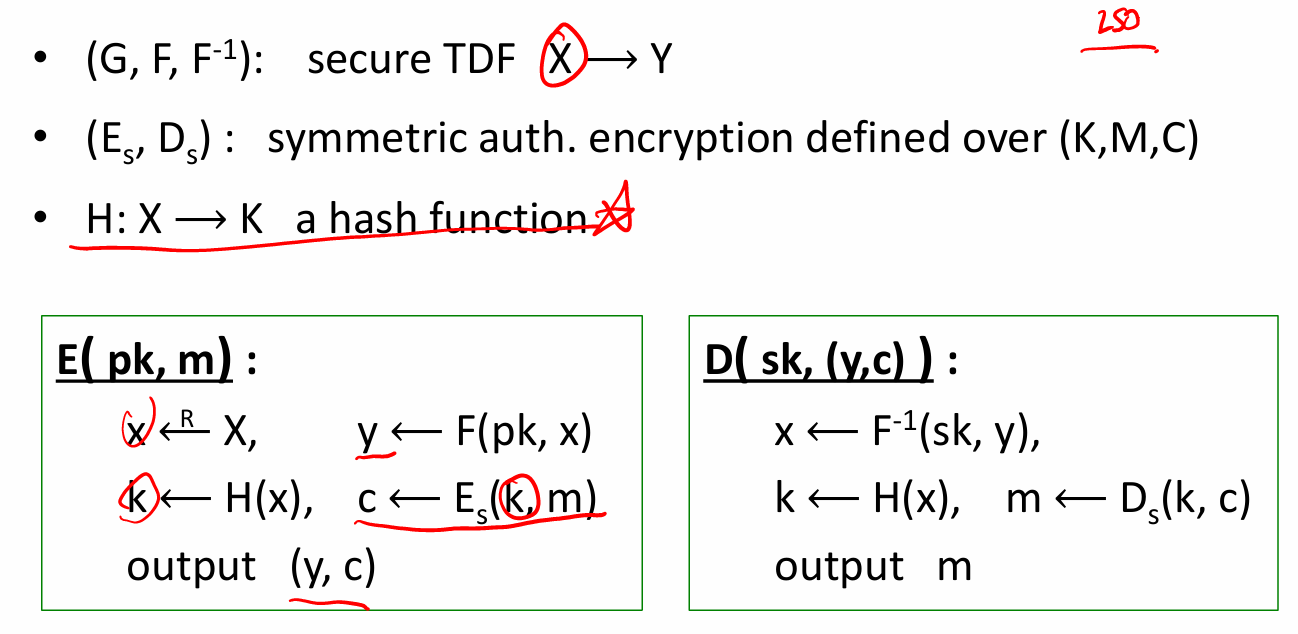
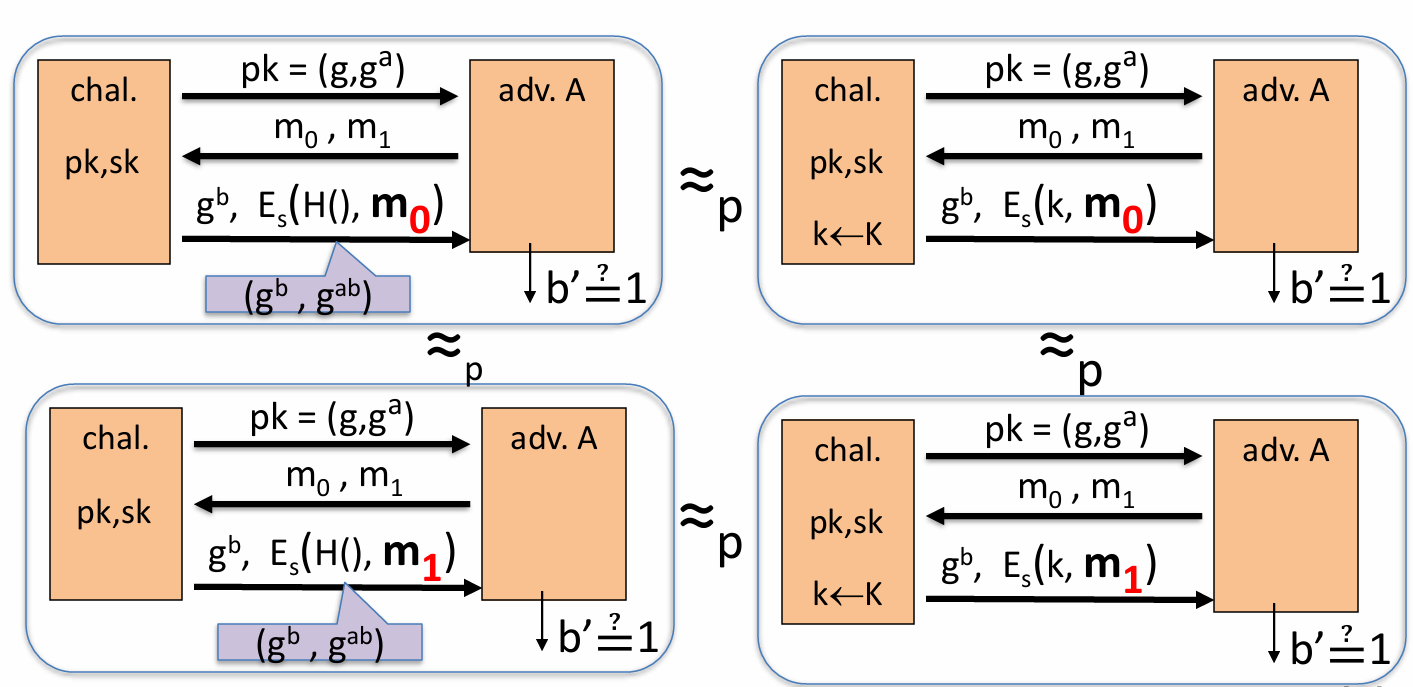
- ElGamal加密系统:(Gen,E,D) Gen生成一个有限群G中的生成元g,以及一个随机的a,a是sk,pk=(g,h=g^a)

- 人话分析加密过程:ElGamal:一个循环群,阶为n,然后选一个g
- 加密:加密者随便选一个b,然后计算gb;然后计算u=hb(g{ab});把gb和g^{ab}一起输入hash函数生成k(hash的输入长度是G,因为g是生成元,生成元的幂都在G里),然后用一个E加密,发送(u,c)
- 解密:
- k怎么恢复?先恢复h^b
- 人话分析加密过程:ElGamal:一个循环群,阶为n,然后选一个g
- ElGamal 的时间消耗:加密需要2 exp (一种提速方法:提前计算好g的各种次方;但是只能一对一);解密需要1 exp
- 密钥交换:
-
ElGamal安全性假设 CPA CCA安全
-
更高安全性的ElGamal变种:twin ElGamal
-
更一般的原理
-
公钥密码体制需要:
- 构造具有特殊性质的单向函数
- 同态特性()和陷门
数字签名
签名和MAC的最大差别:
签名只有发送发可以加密,任何人都可以验证;MAC只有收方可以验证(可以同时确认来源以及防止篡改)
公钥加密和对称加密的区别
公钥加密使用公钥加密私钥解密,任何人都可以加密;对称加密的加、解密使用同一个key
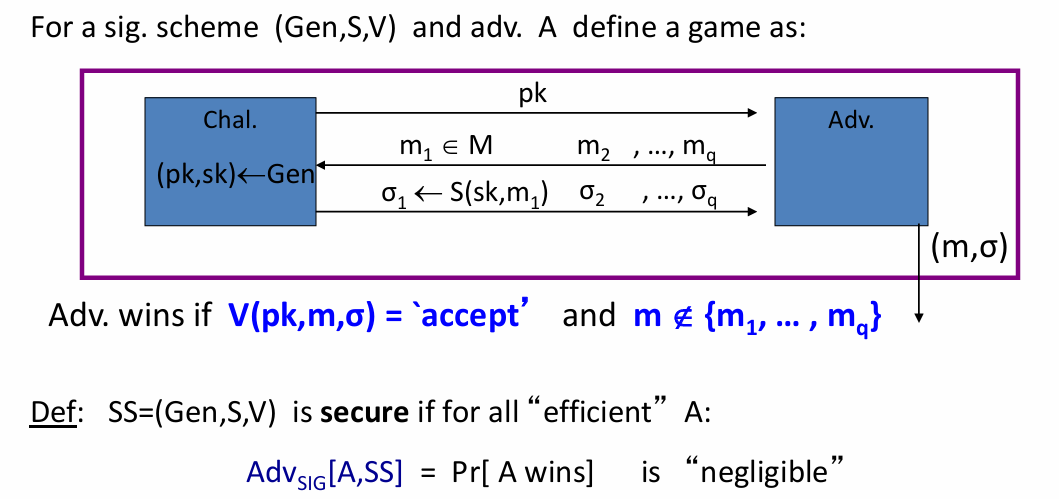
- 数字签名

- 数字签名的安全性
- 数字签名应用
- 代码签名
- 一次性验证通道=>多次验证通道
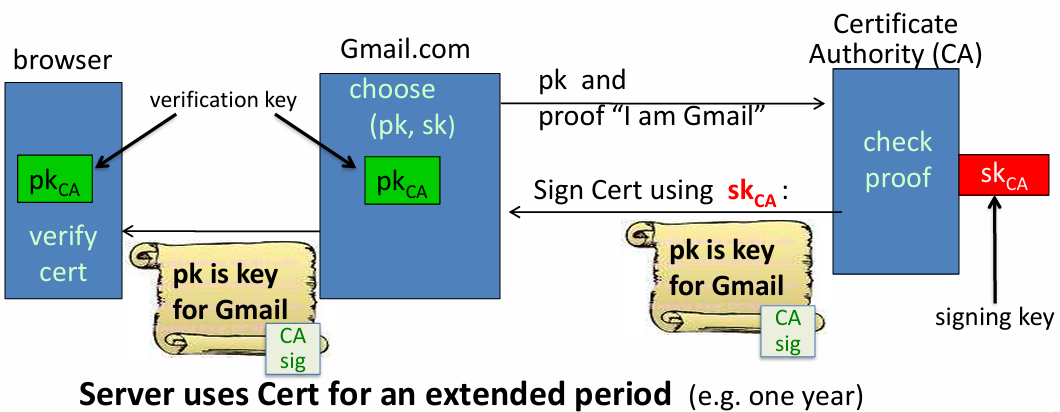
- 重要应用:证书
- 服务器使用可信第三方对公钥签名
- CA生成自己的私钥,用于签名
- 服务器使用证书的时间是有范围的
- EMV payments Credit-card payments
- 对email签名:DKIM
- 邮箱会对每个发出的邮件签名,接收者会从DNS获得pk,在收到邮件之后验证签名的合法性。
- 假设收件人可以为每封收到的电子邮件从DNS中检索新数据,那么Gmail可以在没有签名的情况下实现DKIM吗?可以,Gmail会将每封发送的电子邮件的抗碰撞哈希写入DNS。收件人从DNS中检索哈希并将其与传入消息的哈希进行比较。
- 使用签名和MAC的时间比较
- 如果一个组织签名,一个组织认证:使用MAC
- MAC需要交互去生成共享的私钥
- 接收者可以修改数据或者子集重新签名,在将信息发送给第三方组织之前
- 如果一个组织签名,多个组织认证:使用签名
- 接收者不能更改收到的消息
- 如果一个组织签名,一个组织认证:使用MAC
- 防止数据篡改的三种方式
- 抗碰撞的hash,需要一个只读空间
- 数字签名:需要一个长期的sk
- MAC:提供方需要对每个用户生成以恶新的MAC,同时需要保存一个长期存储的sk生成每个client的MAC KEY
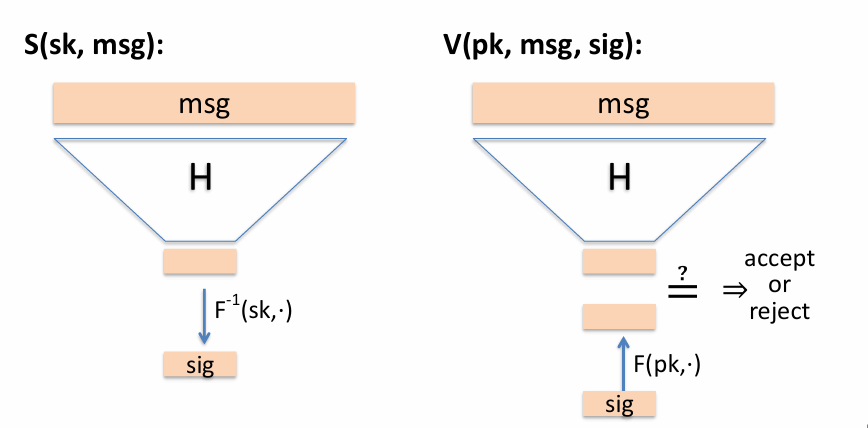
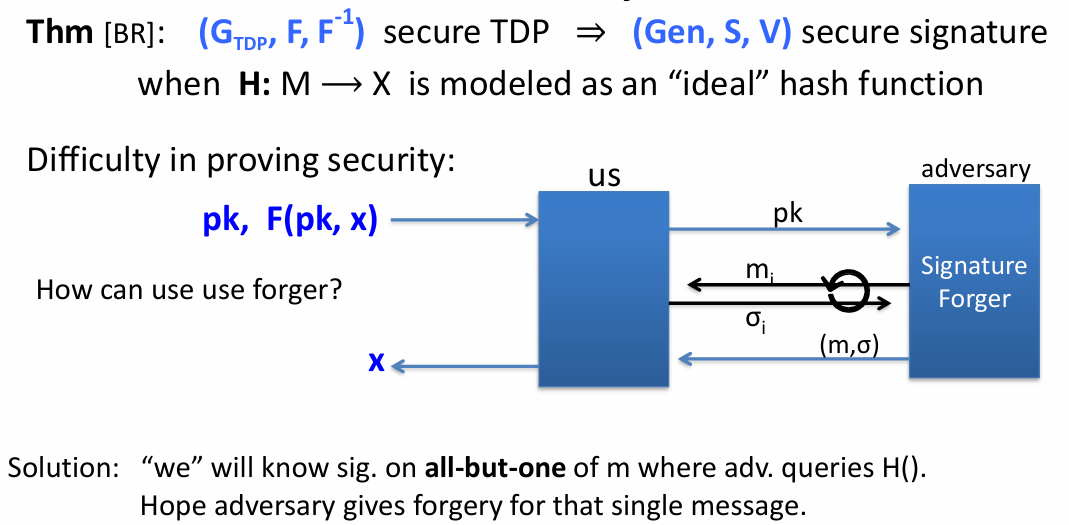
- 数字签名构造
- 使用陷门置换构造签名
现实加密协议
OTP类
- RC4 【不安全】
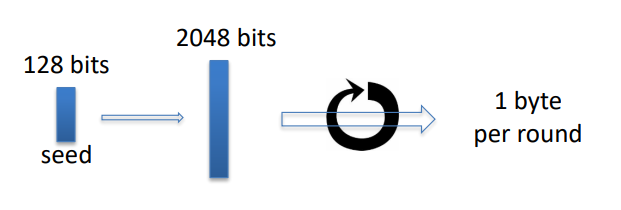
- 初始输入不均匀,比如存在
- 出现连续两个0的概率是
- 密钥之间存在关联
- CSS 【已经被破解】
- CSS基于LFSR:线性反馈移位寄存器
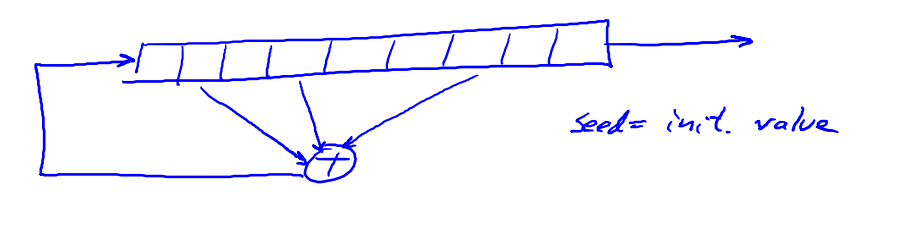
- LFSR的种子是指初始LFSR状态;每次右移一次,末尾舍弃,将异或的结果放在第一位;异或的结果:反馈函数选取固定位置,将这些位置的值进行异或之后再放到第一位
- LSFR的级数指的是LSFR中的寄存器个数
- 作业中出现的LSFR的示例:密钥使用3级线性反馈移位寄存器生成流密码的m和c
- 先通过c和m异或得到k
- k即为LSFR结果,构造f,未知数c0,c1,cn
- 构造矩阵,解方程
- 解得方程与c,根据f推导出k的推导关系
- CSS的加密和解密:CSSseed由5字节组成,前两个字节放在17bit的LFSR 后3字节放在25bit的LFSR
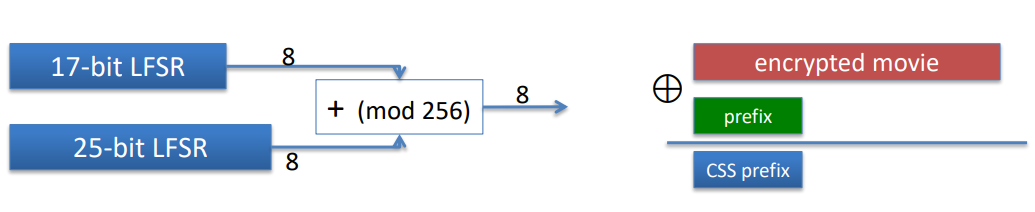
- CSS在2^17时间可破解【如果已知道CSS的前缀,猜测CSS的前17bitLSFR初始状态获得20字节输出,后25bit根据CSS前缀结果反推,验证后25bit是否符合LSFR的输出】
- CSS基于LFSR:线性反馈移位寄存器
- eStream【比较好】
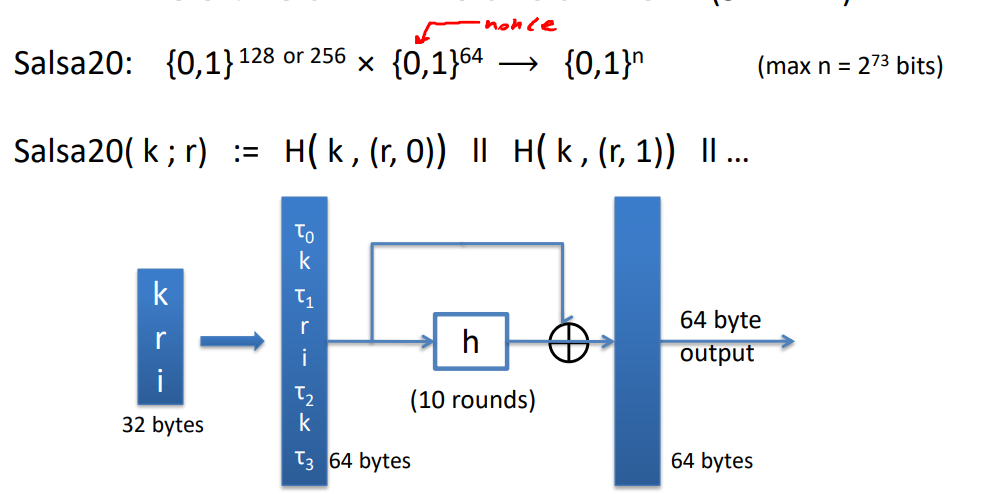
PRG+新鲜值nonce:PRG: 其中,n>>s
R只使用一次,(k,r)永远不会重复==>k可以重复使用 - estream:Salsa 20【安全的】安全性:2^128
MAC
- 使用MAC保护系统文件:每个文件都有一个MAC tag,如果病毒非法篡改了文件中的信息,那么会导致计算出的MACtag完全不同
Hash
- SHA-256
- 构造方法:Merkle-Damgard函数
- 压缩函数:Davies-Mayer压缩函数
- 分组加密算法:SHACAL-2
- TLS协议:使用HAMC-SHA1-96
认证加密
- 现实世界的AE系统以及其构造方式
- SSL:先MAC,生成tag后再将m和tag一起加密
- IPsec:先加密,加密后结果计算tag【永远对的】
- SSH:先加密,然后对明文计算tag,将tag附在密文后面【不安全,泄露明文】
- NIST的认证加密标准:(基于nonce,都是认证加密)

- TLS1.2 (TLS记录协议)【先计算MAC再加密】
- 有两个单向密钥k_{b to s} 和 k_{s to b} ;每个方向维护一个计数器ctr
- 加密 CBC-AES 128 HMAC-SHA1;E(k,data,ctr)
- 先算tag,再pad,再CBC加密,再接到header后
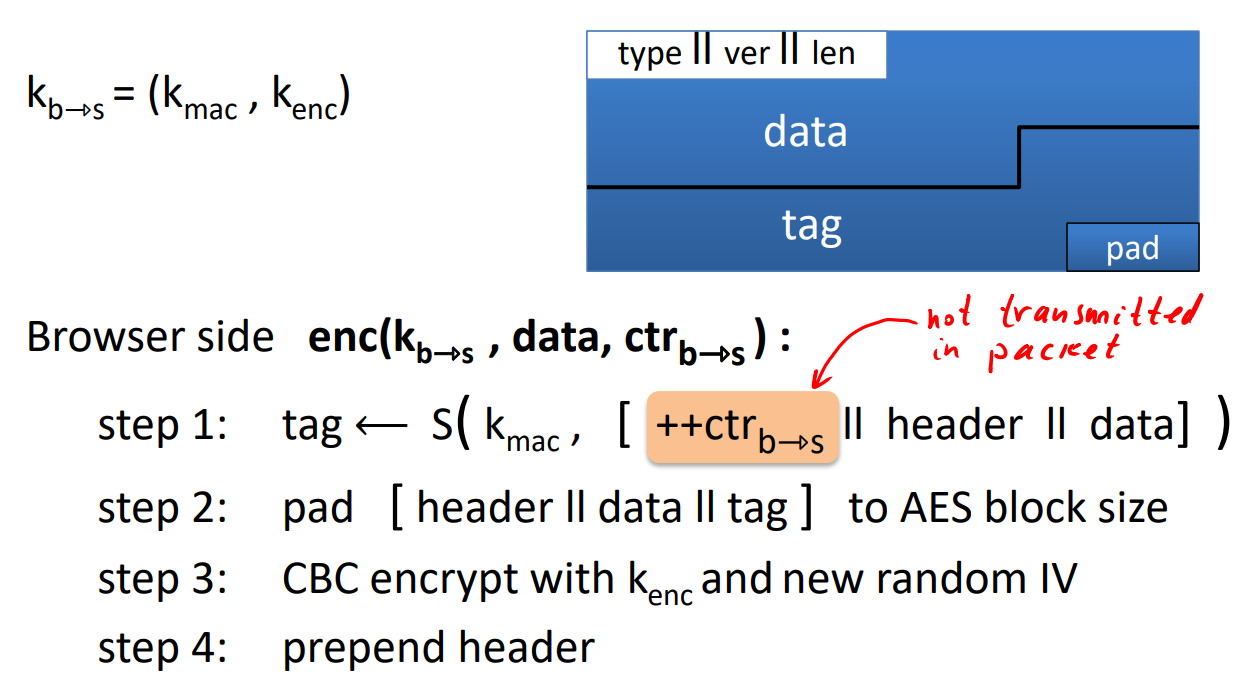
- 解密
- 先CBC解密,pad失败则发送失败;检查tag,检查失败则发送失败

- TLS 1.1漏洞
- CBC的IV是可预测的;下一个IV是本次记录的最后一个密文分块,不是CPA安全的
- 有padding oracle攻击:根据服务器返回的错误消息,可以得知密文的padding是否有效,(对不同的错误会返回不同的响应)
- 长度泄露:TLS头会泄露TLS记录的长度(也可以通过监听网络流量获取)
- 对802.11b WEP的主动攻击
公钥加密
攻击方法汇总
对OTP和流密码的攻击
- two time pad 一次一密,密钥使用两次的情况
攻击者可以根据m1m2异或的结果得到明文信息
- two time pad示例:MS-PPTP
发送方和接收方的key都是G(k),正确方法应该是双方共享一对密钥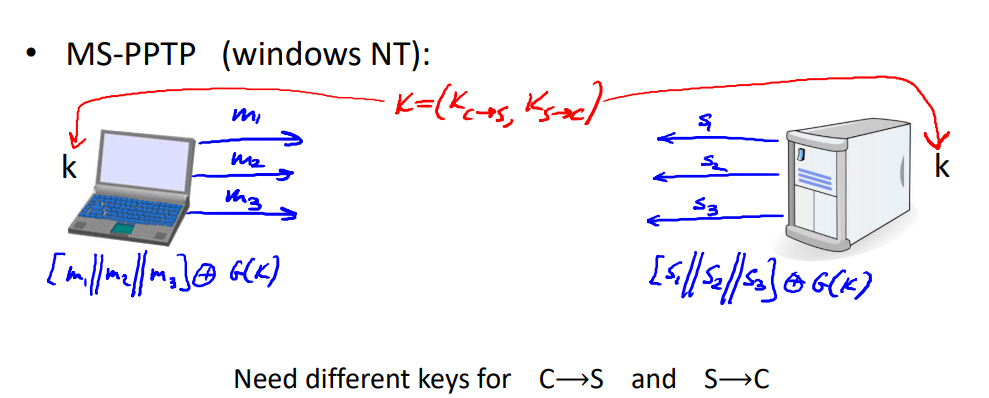
- 802.11b WEP
k不变,IV变,IV24bit,k104bit(不变),在2^24之后,IV会出现重复,且有些802.11会在重复后重置为0===>出现two time pad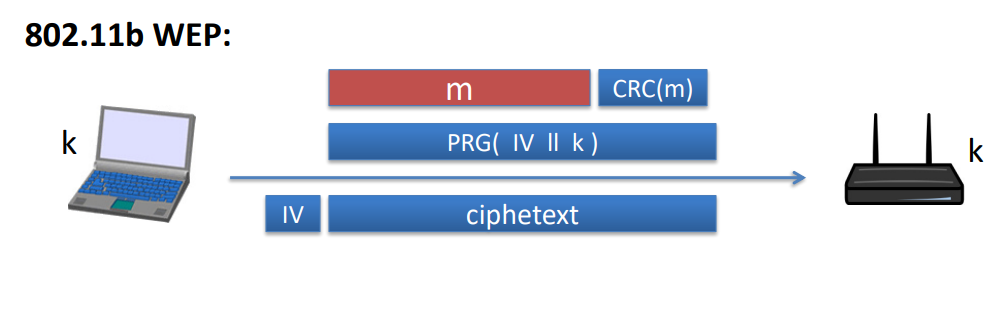
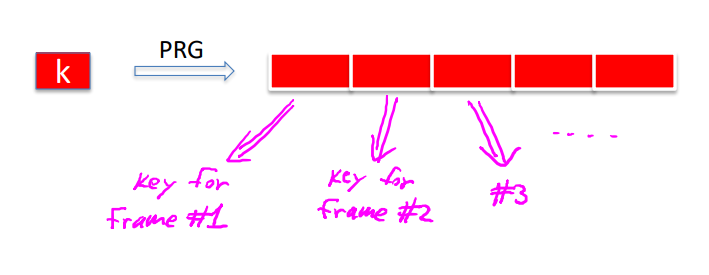
- 解决方法:k作为PRG输入,输出的结果分段,每个分段作为一个key==>每个包有一个伪随机生成的key
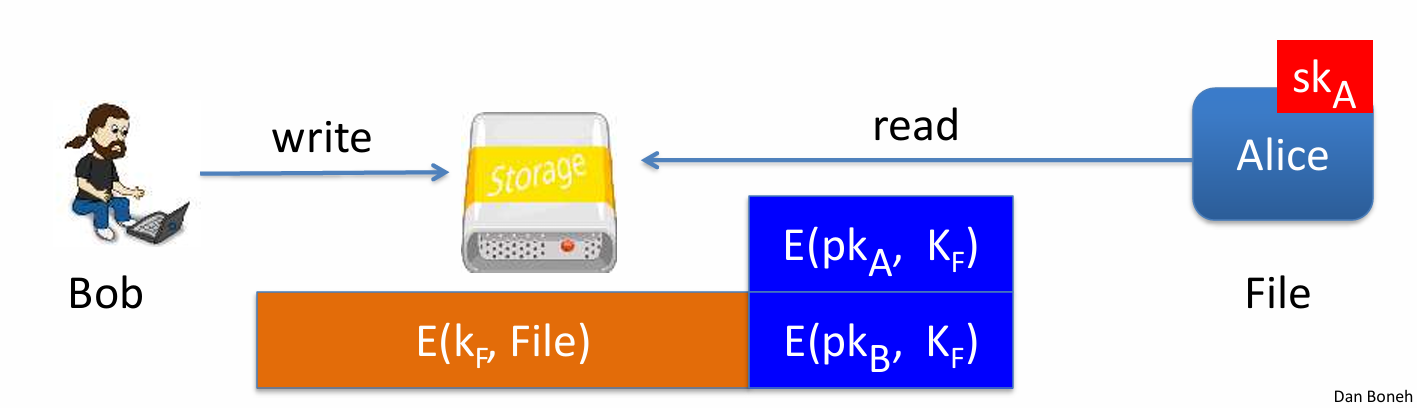
- 硬盘加密
使用相同密钥加密文件,可以根据文件相同的部分破解k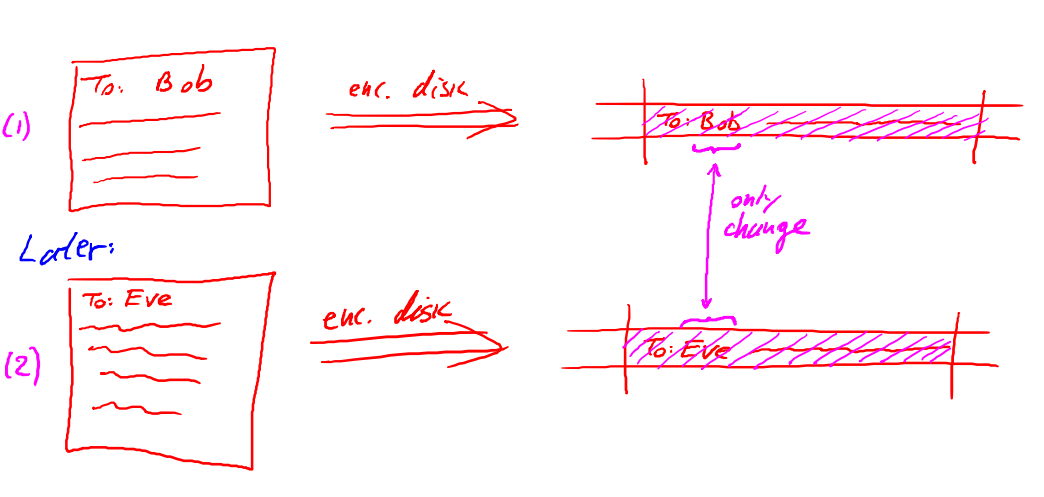
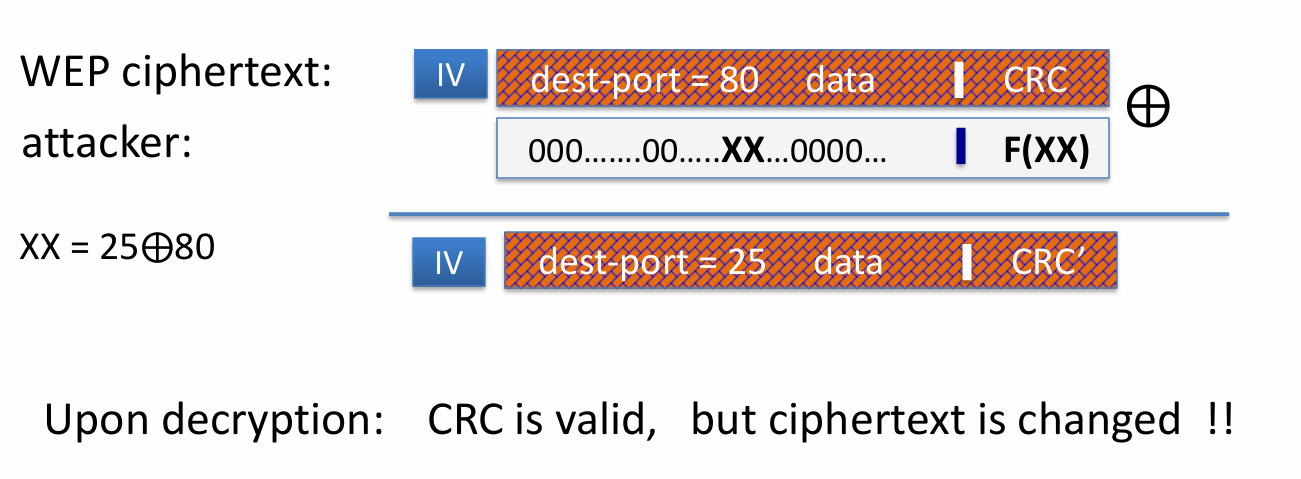
- OTP无完整性、可修改性:修改密文攻击
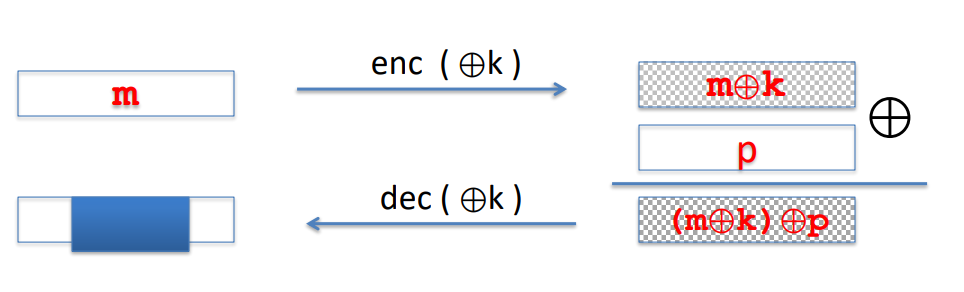 解密后,得到 密文已经被改变但是接收者无法察觉
解密后,得到 密文已经被改变但是接收者无法察觉
攻击举例: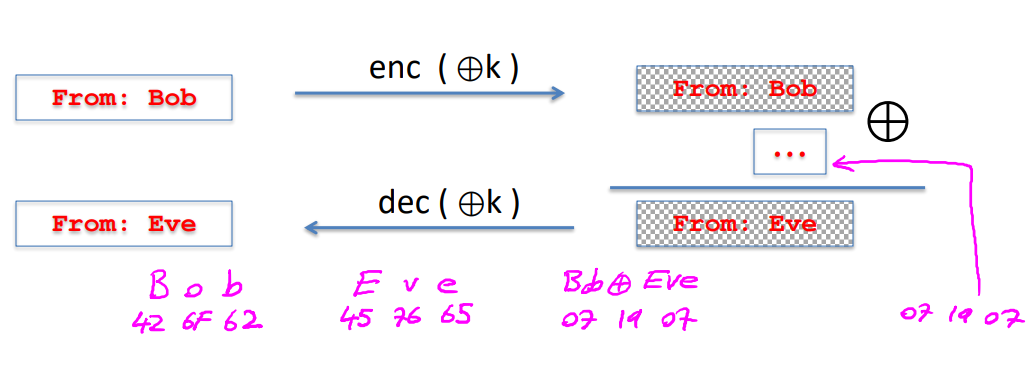
对分组密码的攻击
DES
- 穷尽搜索攻击
- 给定一个key,存在另外一个key,使得DES(k,m)=DES(k’,m)的概率是:256*1/(264)=1/256【即有很小的概率找到key】
- 对于两个DES明文,密文对,他们的唯一性是1-1/(2^71)
- 对于AES 两个输入输出对,唯一性是 1-1/(2^128)
- 对于3DES 穷尽攻击的时间是2^118
- 2DES的穷尽搜索攻击(中间相遇攻击) 考过
- 一条消息就可以实现穷尽搜索攻击
- 2E((k1,k2),m)=E(k1,E(k2,m));key长度:112bits 密文长度64bits
- 寻找(k1,k2),使得E(k2,M)=D(k1,c)

- Step1:构建表格:列出所有k2以及对应的E(k2,M),并且按照第二列的值排列(方便第二步寻找)
- Step2:尝试相遇:列出所有的k,尝试D(k,C)是否在刚刚的表格中的第二列中,如果找到,则输出对应的(k1,k2)
- 时间复杂度:2个
- DESX的穷尽搜索攻击(中间相遇攻击)
- EX((k1,k2,k3),m)= k1 xor E(k2,m x or k3 )
- 一条消息不能实现穷尽搜索攻击(因为始终不能确定k1或者k3),应该使用两条明文,密文对进行相遇
- Step1:穷举k1,计算k1 xor c1 以及 k1 xor c2
- Step2:穷举k2,计算 D(k2,k1 xor c1) 和 D(k2,k1 xor c2)
- Step3:计算D(k2,k1 xor c1) xor m1 以及 D(k2,k1 xor c2) xor m2,如果相等则相遇,计算结果为k3
- 测量时间攻击,测量功率攻击;错误攻击:检测错误
- 线性密码分析:DES的S盒设计缺陷导致
- 量子攻击
- 对于搜索问题,普通计算机需要O(|X|)的时间,而量子计算机只需要O(|X^1/2|)的时间搜索
AES
- 针对AES-256,存在相关密钥攻击,该攻击可以在给定 2^99个输入输出对(它们是由4个相关密钥加密而成),可以在 2^99时间内恢复密钥
- 对可预测IV的CBC的攻击
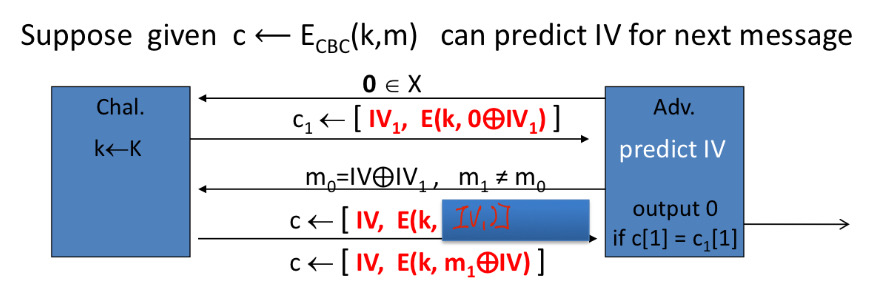
- 构造一个全零的,可以判断异或的值
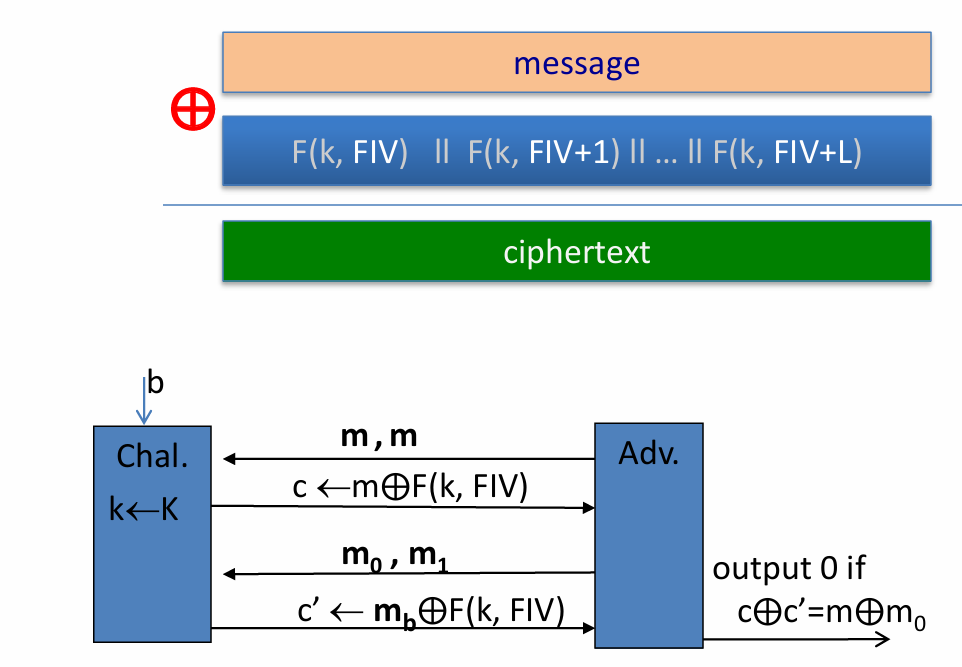
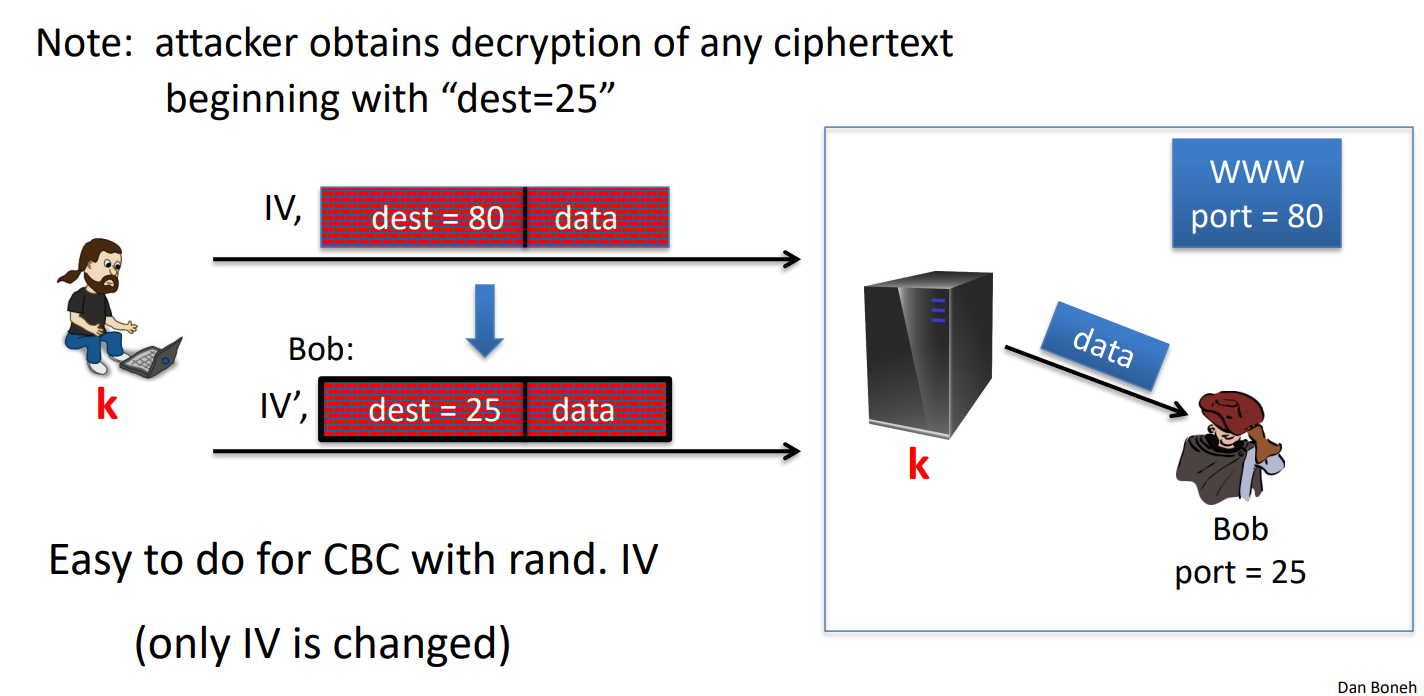
- 针对带随机IV的CBC进行篡改攻击【作业里有】【随机IV的CBC不提供认证加密】
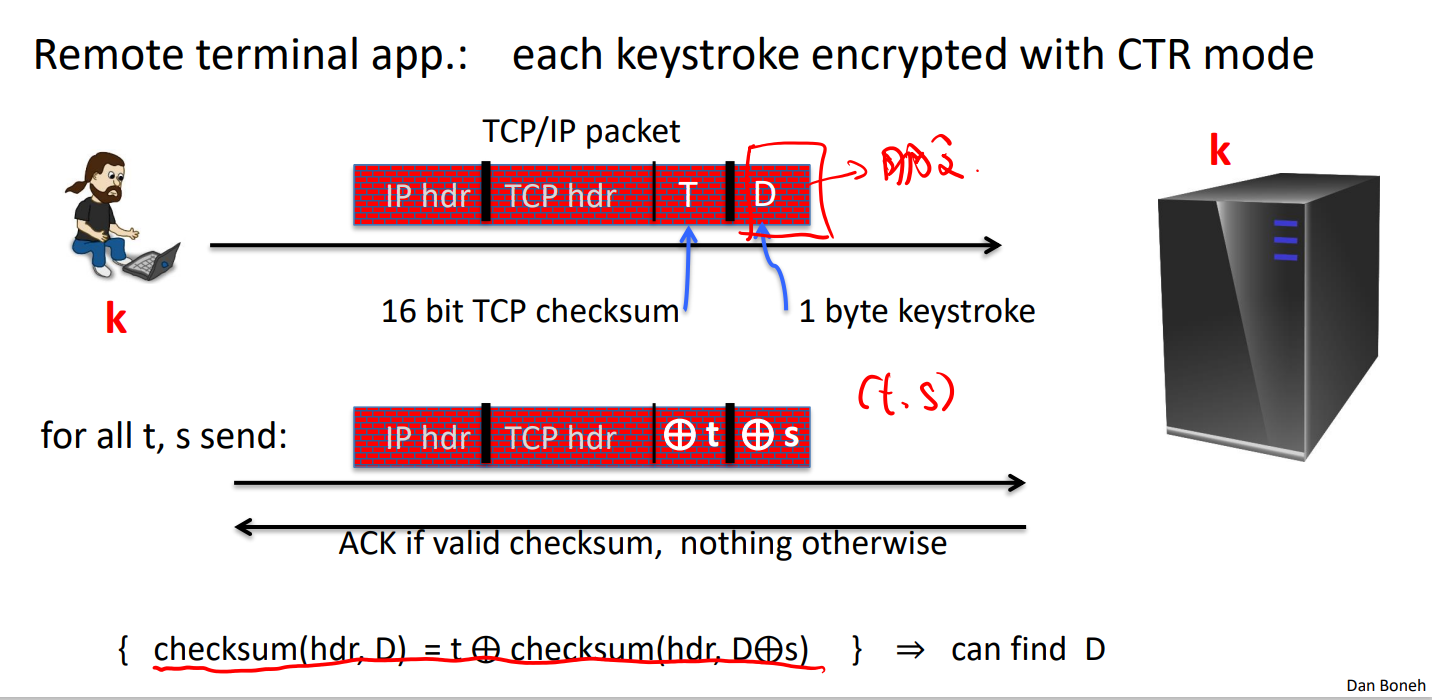
- CTR模式的选择密文攻击
对MAC的攻击
- MAC的安全边界
- CBC MAC填充攻击:如果是应用全0填充,那么攻击者可以通过构造消息末尾为全0的消息,并且提前询问攻击者消息的加密,pad(m)=pad(m||0)
- 对MAC认证的计时攻击
- 产生原因:
HMAC(key, msg) == sig_bytes该代码在验证tag的时候,由于是逐个字节比对,可以根据时间来确定哪些位数是对的
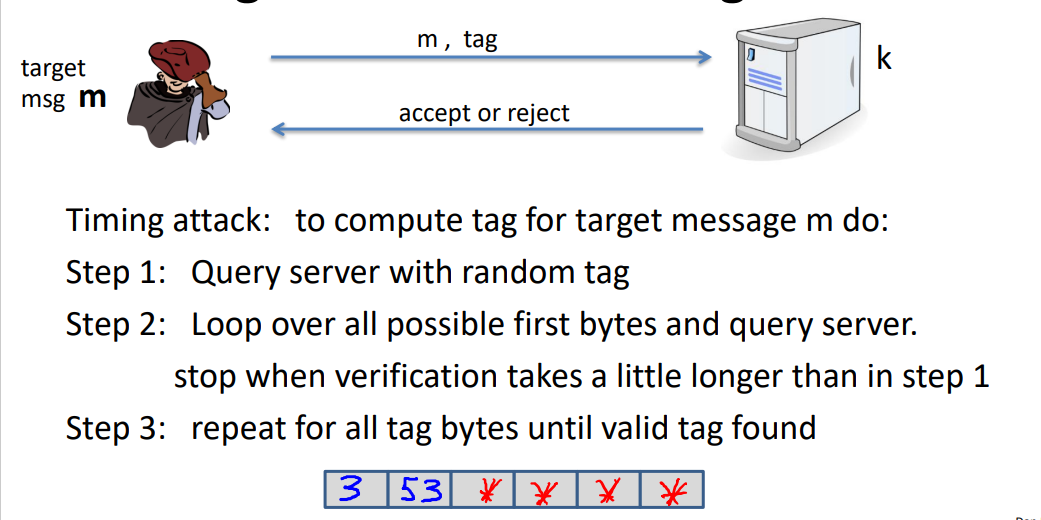
- 解决1:让比较总是花费相同时间
- 解决2:不让攻击者知道哪个值被比较了
- 产生原因:
对Hash的攻击
- 通用生日攻击
- SHA
- SHA1 不安全,输入160bits 通用攻击2^80
- SHA256 安全 输入256bits 通用攻击2^128
- SHA512 安全,输入512bits 通用攻击2^256
- 量子计算机优化
对认证加密的攻击
对padding的攻击
- Padding Oracle可以通过先加密再MAC避免
- 先MAC再加密虽然提供认证加密,但是只有在不透露解密失败原因的时候
- 计时攻击:根据返回错的时间判断错误类型
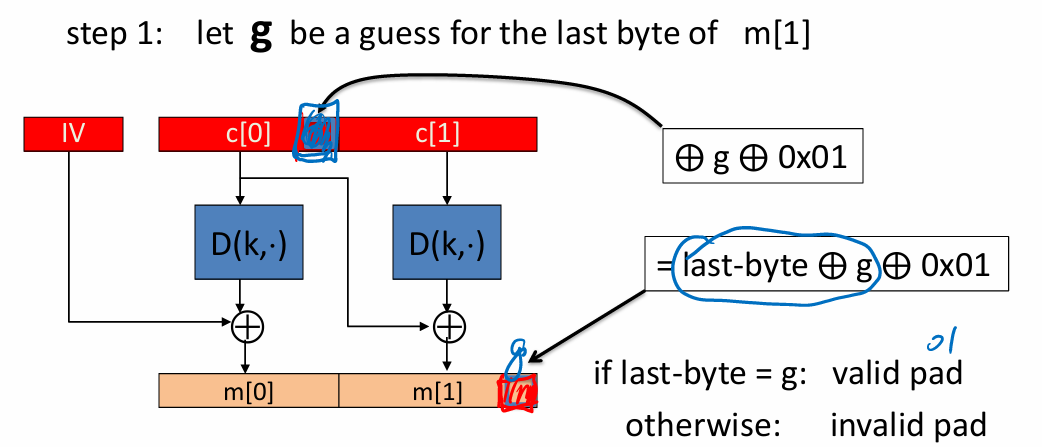
- 针对CBC的padding oracle攻击
- 对TLS实现IMAP的padding oracle攻击
- 问题:TLS会在每次获取不合法消息之后重新协商key
- 每五分钟客户端会向server发一个登录密钥
- 攻击者还是可以通过padding oracle恢复出用户明文
非原子操作的解密攻击
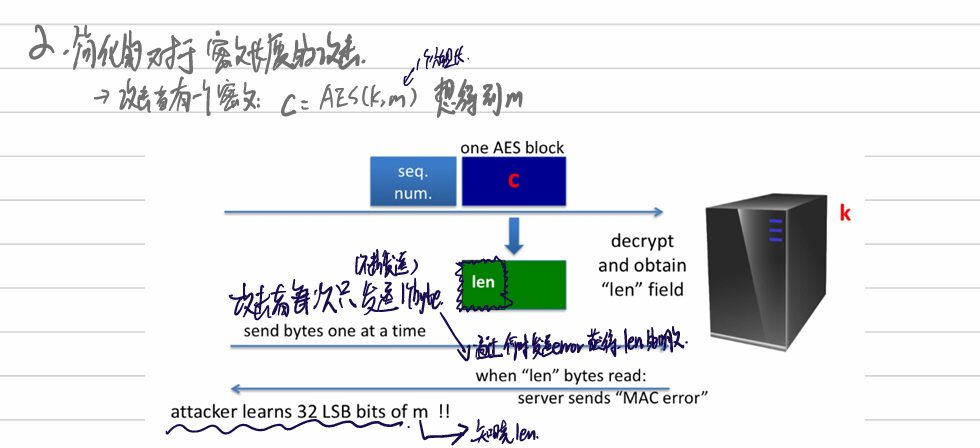
- SSH二元包协议攻击
- 协议:先解密长度;再读取对应长度的包,然后解密密文分组,最后检查MAC是否合法
-
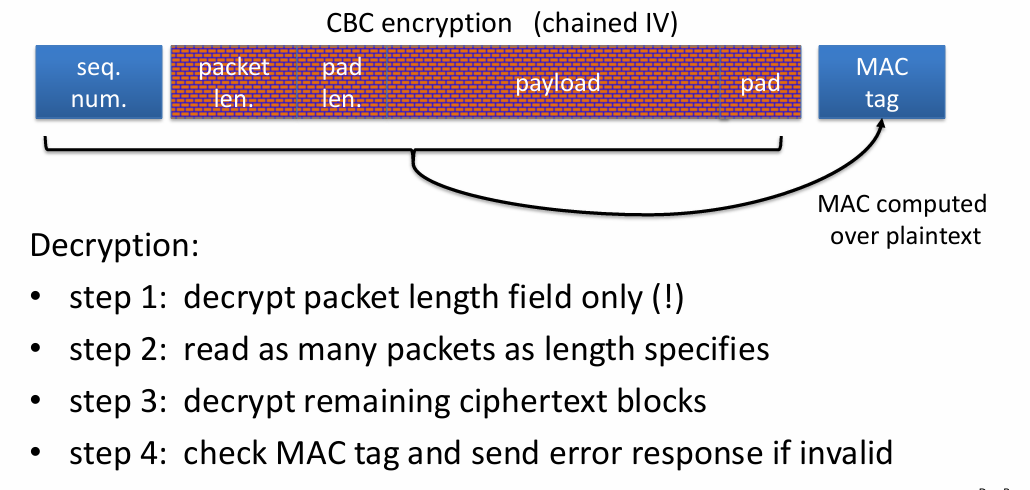
- 攻击:通过发送的“MAC error”判断消息m的长度,发送一个大小只有1的m,server先解密得到len,之后试图从收到的信息后获得len长度的消息,此时攻击者一个字节一个字节地发送消息,并且等待server发送“MAC error”(表示消息长度是对了,但是没有通过MAC的校验)====>攻击者获得明文中len的信息
- 非原子操作的解密,以及在正确认证之前就使用解密内容是不安全的。
- 如何更改SSH?
- 直接使用明文的长度域(可以防止CCA)
- 单独对长度(seq-num,length)进行MAC验证,加在len明文后
- 将先加密+MAC改成先加密后MAC没有用,因为还是会泄露长度域
- 可以更改长度域名,通过每次收取一个字节信息就用MAC来识别包的边界,可以但是要花费大量时间
对公钥加密的攻击
对RSA的攻击
- 计时攻击:计算c^d(mod N)的时间可能会暴露私钥d
- 功耗分析
- 解密错误攻击(比如,检查解密错误,可能会重新计算一下解密后的密文和收到的密文是否一样,这个耗时会暴露d)
- 举例:CRT-RSA中国剩余定理RSA(如果计算xq发生错误但是xp没有,那么就可以计算出p)
- 举例:RSA密钥生成问题:如果使用同样的p生成RSA密钥,那么则会导致不同设备的N有相同的因数p
第八周随便提一点
考试形式:闭卷考试,题型:填空题(20分)选择题(20分)大题4道,每道题15分左右,选择填空一般是零散的知识点,如OTP的密文如何得到对应明文,如何解密;
算法安全性:如作业中的,哪些哈希算法是安全的,,3des安全吗,AES安全吗,md5安全吗,sha1安全吗 sha256安全吗;认证加密,如果随机初始向量CBC模式,先加密后认证安不安全;公钥;;;
答题:会有简答题:概念性的东西,公钥加密和对称加密的区别和概念,有对称加密为什么还要有公钥加密;如果用纯对称的做密钥交换,代价很大,gap最多是n^2 如果有公钥加密,gap会达到指数
从定义上来说,对称:直接加密消息;公钥加密,用于传输
简答题,提一些协议的漏洞,TLS的漏洞,padding oraacle攻击,什么pp协议,WAP协议的漏洞讲一下上课讲过的漏洞
大题可能和作业有些类似,内容更多,成体系的东西比较多;建议看确定性加密
TLS协议一定要考 讲了很多TLS
考试:考过Dlog原理的hash抗碰撞
上课透了::::注意公钥加密的CPA安全性的定义
补充了:群签名的例子:给所有的用户相同的私钥
第十周:回顾
- 秘密共享;Shamir秘密共享是怎么做的。(不会考证明,但是会考公钥加密CPA安全性)门限秘密共享怎么利用拉格朗日插值;(n,t),给定t-1个点可以重构,t个点不能
- 流密码:
- OTP的定义;根据消息和密文恢复密钥
- 流密码将OTP变为实际可用的(伪随机生成器:安全性要求【不可预测性】)
- 攻击:PPTP协议的问题;WEP的问题(至少三次的问题,到底有哪些脆弱性,理出来);OTP完整性攻击(篡改密文 from bob from eve );
- RC4的缺陷(WEP);Salsa20的构造(很无聊,知道他是安全的;要知道哪些流密码是安全的哪些是不安全的;标准化的东西记住也没有用)
- 语义安全性:不会考太多,没有太多有关语义安全性的证明题;更多是分析以及找到一些攻击
- 证明的部分不用花太多时间,要理清楚他们之间的关系:(异或);攻击比较容易考(11:39)
- 攻击多看
- 第十周应该要提一点了吧
Dan Boneh Problem Set
Week1
- 判断安全的PRG
- 选项1:A:区分首位是不是1,Adv=1/2
- 选项2:如果G’可以由A区分,则G也可以由G区分(异或1,分布不变),与题干矛盾
- 选项3:k是随机选取的,异或1,分布不变
- 选项4:判断LSB是不是等于0,Adv=1/2
- 选项5:去除最后一个bit,不影响G的安全性
- 选项6:判断第一个bit和第n+1个bit是否一样即可

- 判断一次性的语义安全
- 选项1:询问 和 可以区分EXP(0)和EXP(1)【全0,和全0接一个1,如果全0,那么输出结果最后一位肯定是0,另一个m,输出结果最后一位肯定是1,Adv=1】
- 选项2:如果E’不安全,则E也一定不安全,与题干矛盾。(我也不知道为什么,但是感觉就是对的)
- 选项3:不能上当了,虽然这个很随机,但是直接把key接在E后面,攻击者直接可以用k解密
- 选项4:输出两次密文:攻击者无法获取任何信息,如果要破解E’,必然要先破解E。(不能把他和真随机比,因为这是语义安全性,不是在判断PRG)
- 选项5:加不加0对攻击者都没有影响,因为加0这个行为其实没有暴露可以区分m0和m1的方法
- 选项6:破解攻击很简单,构造 和 全0输出还是全0,全1输出是全1 Adv=1

Week2
- 判断安全PRF
注意看,正确的选项都是直接用了安全的PRF,直接输出,都可以将他们转换为真随机,转换后的结果仍然是真随机
- 两轮Feistel网络
根据提示,攻击方法如下:

- 基于Nonce的CBC,但是Nonce用和加密一样的key k作为PRP的输入
因为有点简单,就是列举一下,不写过程了
- CBC加密长度为l个分组的密文,如果第l/2个分组出现问题,会影响2个密文的解密;CTR模式,同样长度为l但是第l/2个密文出问题,只会影响一个密文的解密
Week3
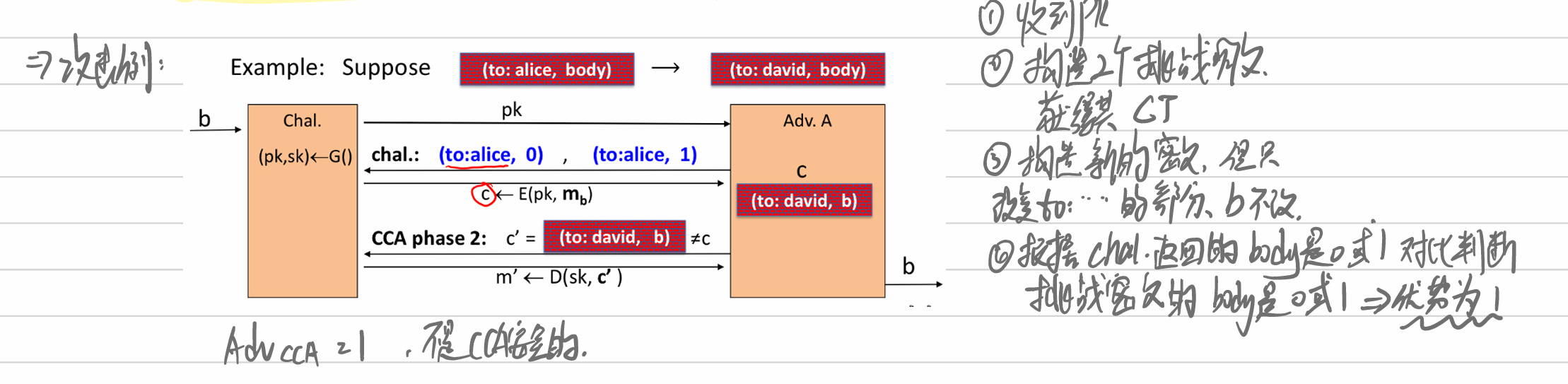
- 这题,不太理解,感觉都不对,难道选第一个选项是对的?只有更改了文件内容才会认证失败,难道更改名字不会失败吗
- MAC的安全性


- ECBC-MACB使用固定IV的攻击:
- 使用r作为初始向量,通过对IV异或可以做到更改m的目的

- 这题说的是把消息m的最后一个bit进行更改,加解密需要使用AES的次数,记住CBCMAC需要加密两次;这题要先把原消息m的最后一个分组解密,然后再更改成m’,再加密
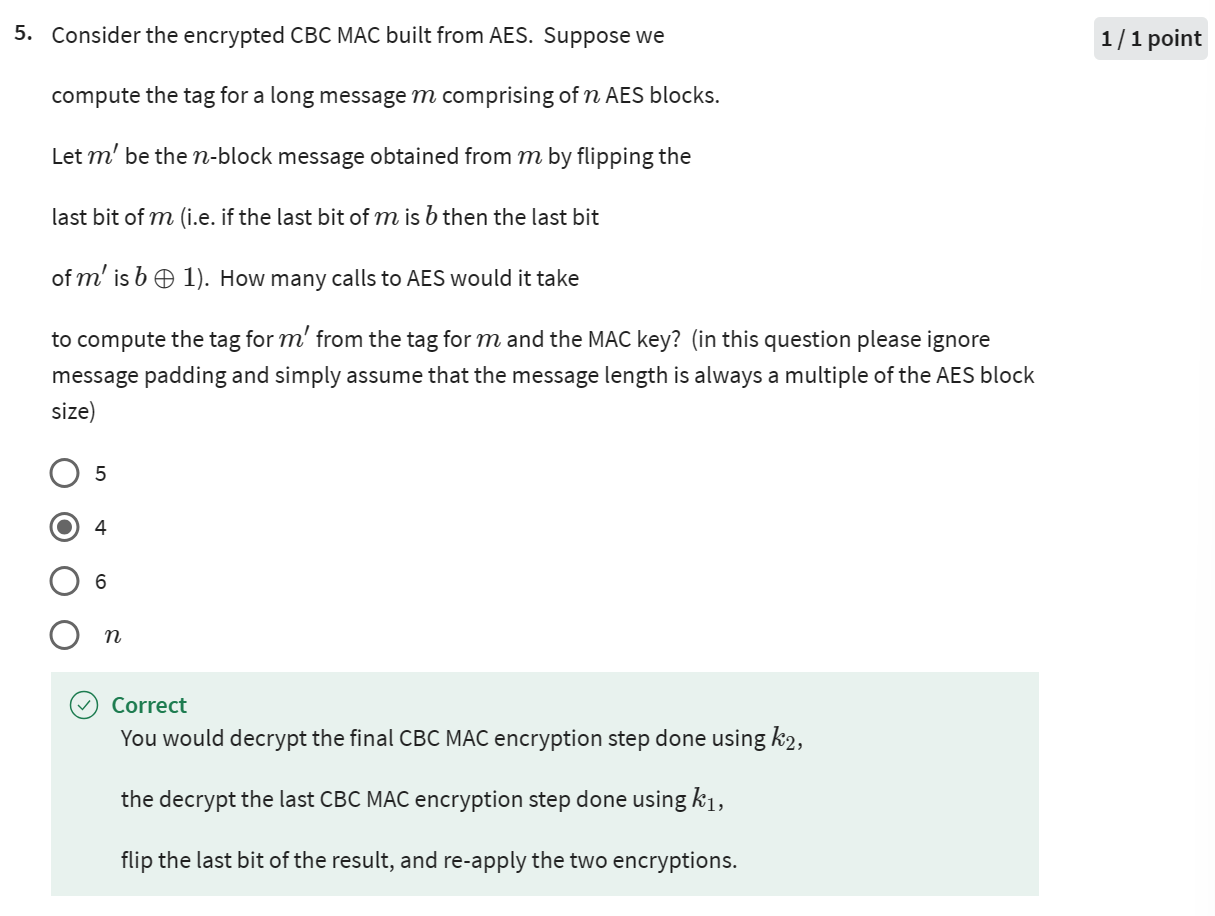
- 抗碰撞
- 32次方太短了,可以在 2^16时间内攻破

- 碰撞需要的样本数量计算
- 2次碰撞:T的大小是tag空间,如果两次碰撞,只需要尝试 个消息即可
- 3次碰撞:假设需要n个样本,n个样本的三层碰撞的组合有 种,由于两个H函数的碰撞概率(H(x)=H(y))为 ,构造三层碰撞需要 H(X)=H(y);H(x)=H(z)同时成立,同时成立的概率是 则三次碰撞的概率是 由于需要概率趋于1,这里不妨直接令 则可以计算出,需要


Week4
- 经典针对CBC的完整性攻击
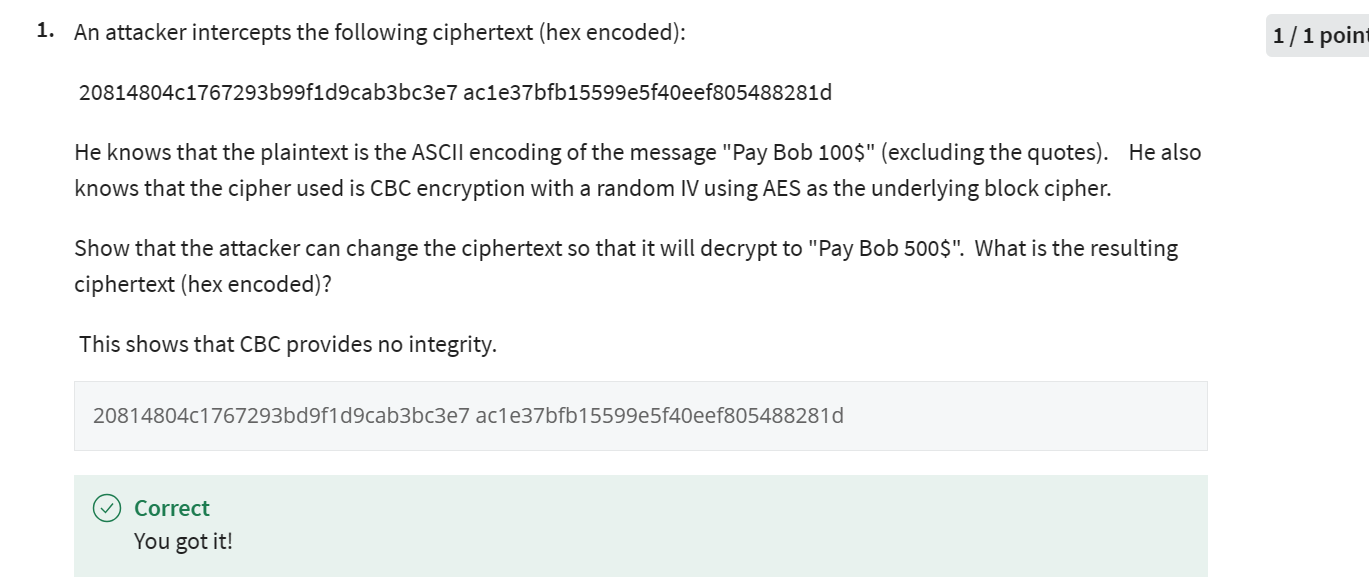
- 判断认证加密
- 认证加密提供CCA安全,同时也满足many time key的安全

- 如何通过对称加密构造一个MAC?==需要对称加密满足认证加密的要求(MAC安全,则MAC需要不能被存在性伪造,由于认证加密不存在存在性伪造,因此MAC也不会存在存在性伪造,就是安全的MAC了)

- KDF,奇怪的题目,让你挑一个在k均匀分布的时候安全但是在k不是均匀分布的时候不安全的PRF

- 什么情况下可以使用DAE(确定性认证加密)

- CBC攻击的次数
- 每个bit攻击2^8=256次*48个字节=12288次

Week5
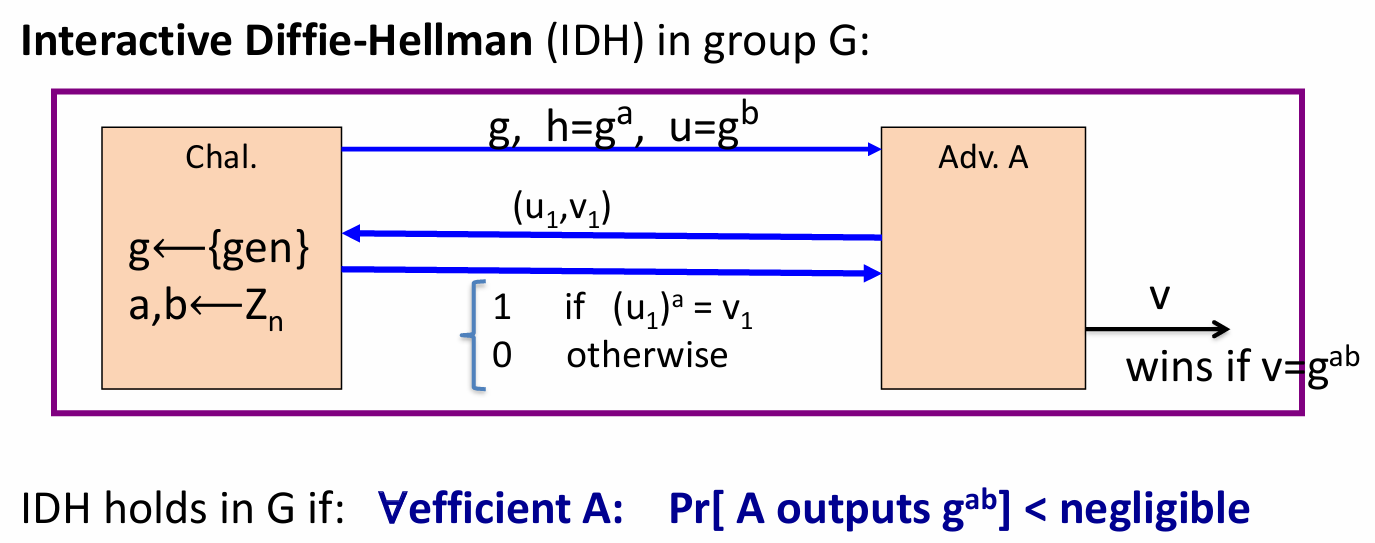
- 利用DH问题难解的性质
- 如果DH难解,那么由DH组成的f也一定是难解的

- 别搞反了:只要记住A只知道a,B只知道b就可以
- 玩具协议加MAC可以防止中间人攻击吗?
- 欧拉定理和费马定理计算阶乘应用
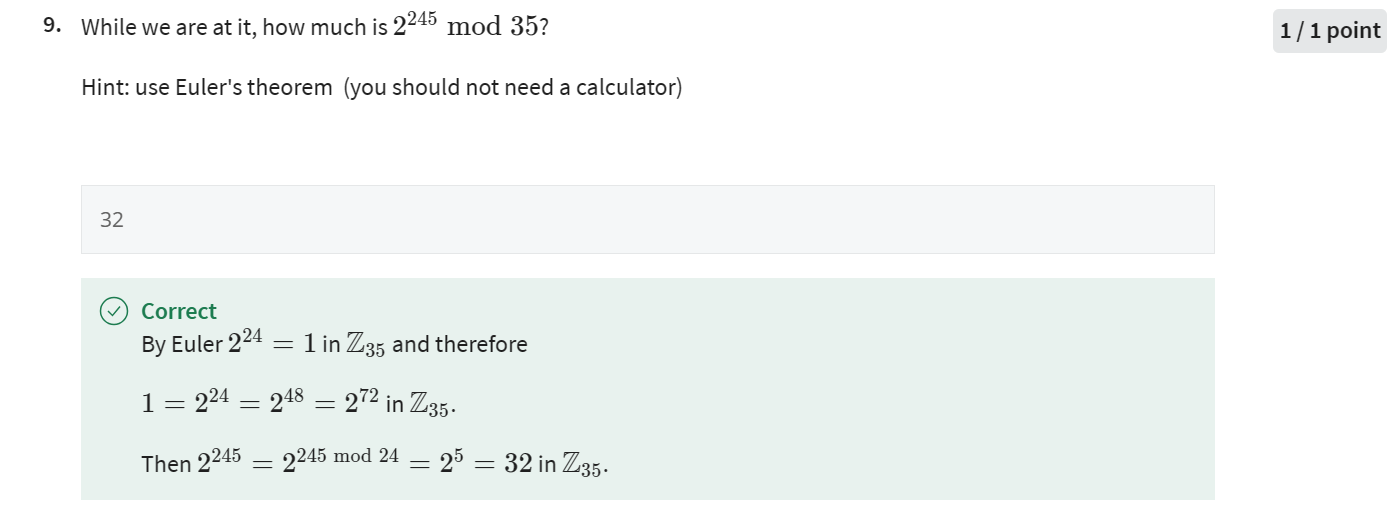
- 解得方程
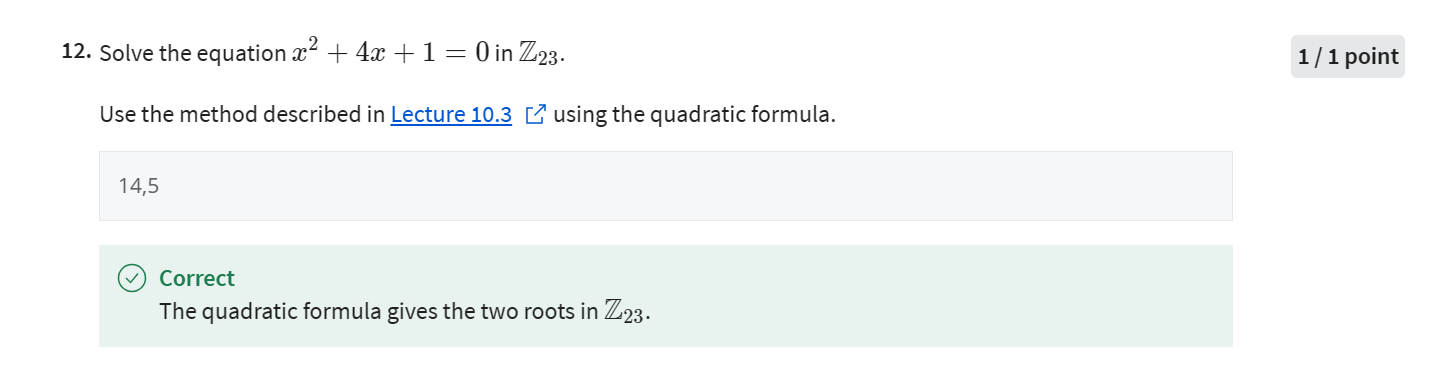
Week6
- 公钥加密可以像对称加密一样,加密后的结果是32bit吗?
- 公钥加密(Gen,E,D)使用的加密算法E可以是确定性加密吗?
- 判断安全的公钥加密系统
- 使用y分解N????【很迷惑的一道题】
- 找到一个偶次方根不为1的

- N分解三个素因数

- N由三个相同的相近素数产生,那么d的边界是???【没搞懂这道题】
- 边界是1/6,是因为N-fai(N)现在是N^{2/3}的秩


Week7
-
一个均匀分布s和一个随机数异或是0,那么概率就是1/2^{n}

-
各种安全性的梳理
- 完美安全:密钥长度一定要大于等于消息长度
- 语义安全性(一次密钥的语义安全性质):只能询问一次m0,m1
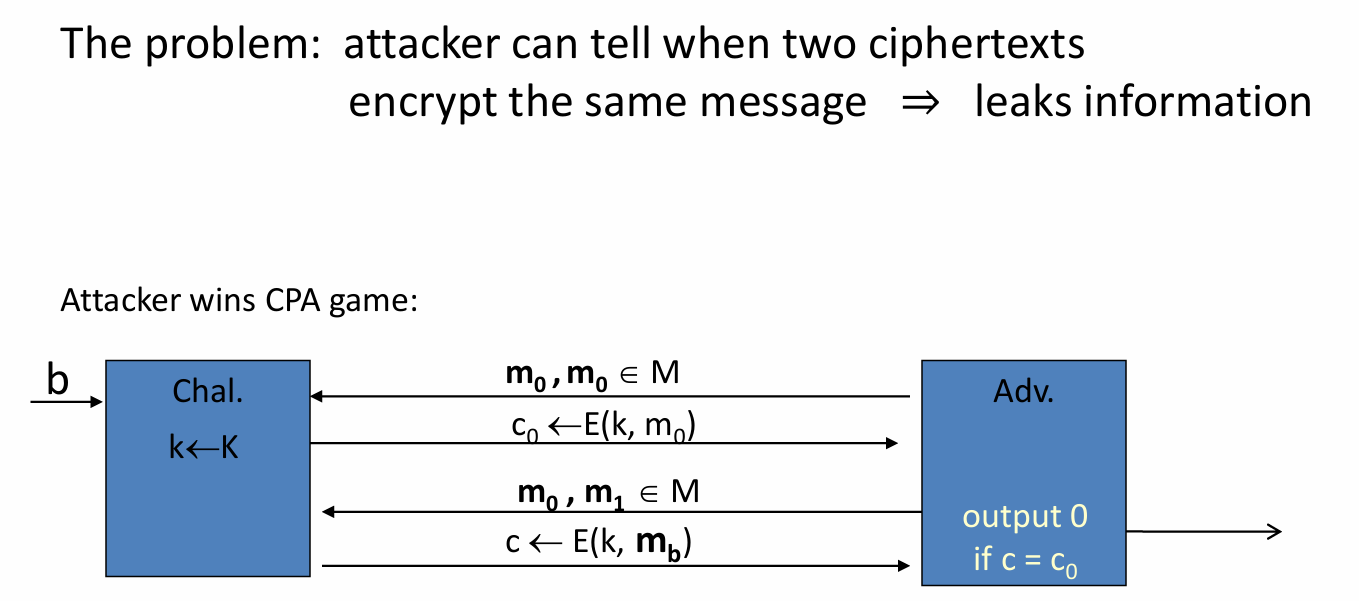
- CPA安全:many time key 可以进行多次询问,每次询问的结果用一个key加密而成,随机获得0,1里的一个值的加密。确定性加密一定没有CPA安全
- 确定性CPA安全:cpa安全的基础上,限制加密者不会加密相同的明文两次
- CCA安全:可以无限询问密文的解密,但是只能询问一次m0,m1的加密内容,目的是要猜出是m0还是m1的加密

-
CBC用PRP,CTR用PRF
-
不懂但是做对了:对使用一个key去加密2^32个消息的对称加密,如果需要使其具有CPA安全,那么需要应用新鲜值,新鲜值的长度?
- 原因是用了生日攻击??
- 不太懂啊啊啊

-
不懂但是做对了;为什么计数器模式可以只用32bit长度的nonce,但是不用计数器的需要2^128
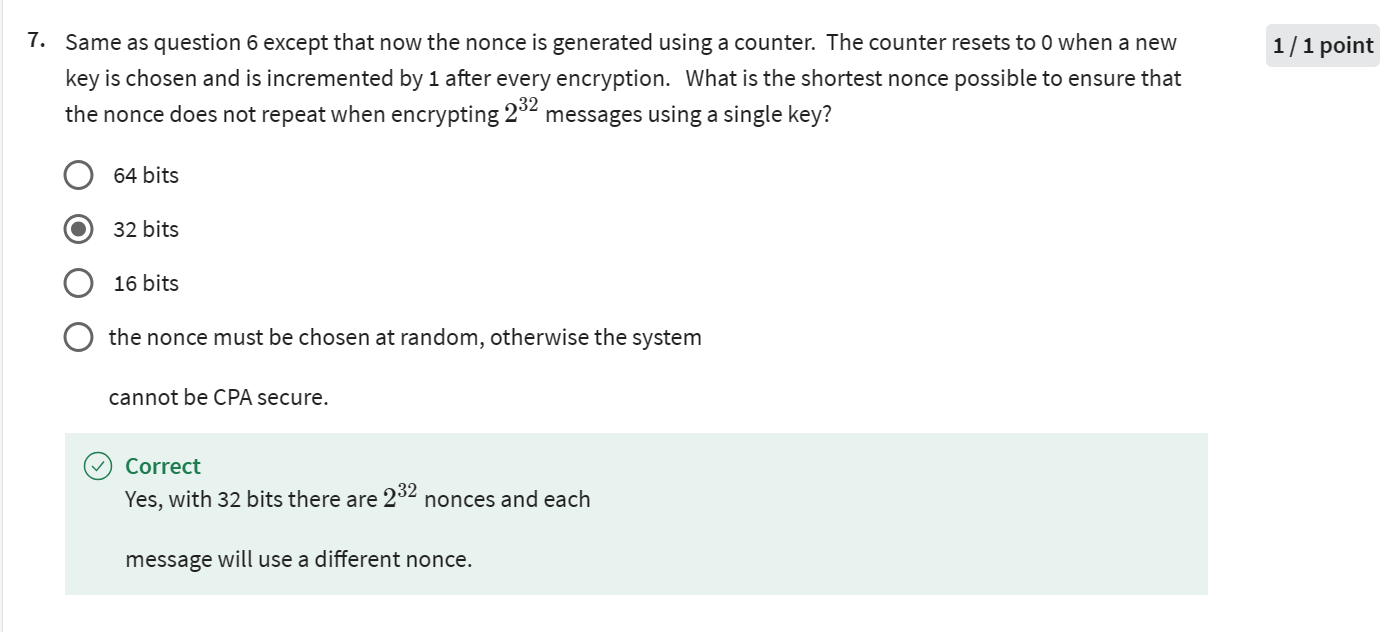
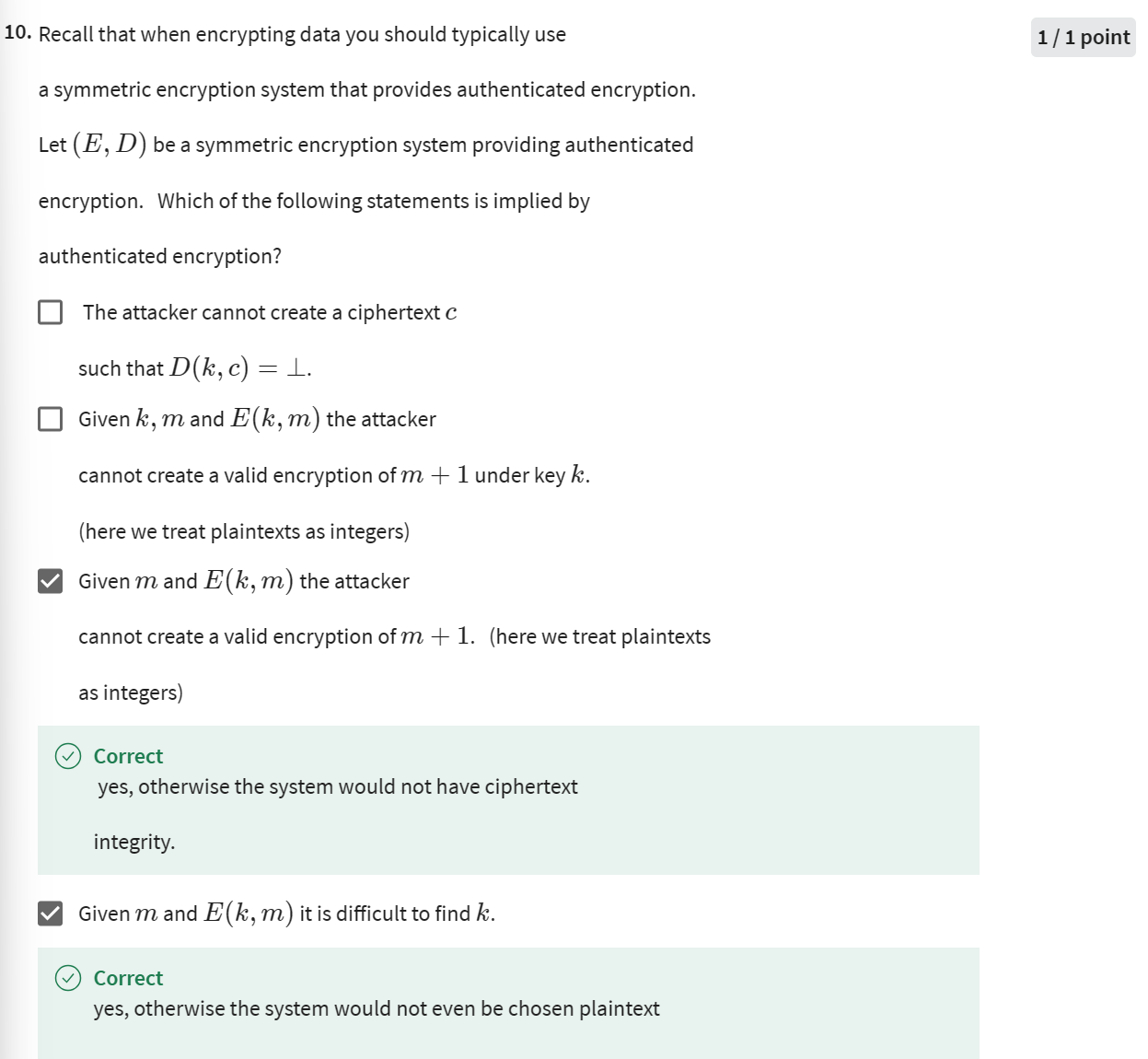
-
安全的MAC的定义
- 为什么是给定一个k,后半句可以理解

-
碰撞检测的定义

-
语义安全的定义
-
DH密钥交换协议

密码学透透🤣
开源精神互相帮助捏
====秘密共享
- Shamir秘密共享是怎么做的。(不会考证明,但是会考公钥加密CPA安全性)门限秘密共享怎么利用拉格朗日插值;(n,t),给定t个点可以重构,t-1个点不能
====流密码
-
OTP的定义;
-
流密码将OTP变为实际可用的(伪随机生成器:安全性要求【不可预测性】)
-
攻击:PPTP协议的问题;WEP的问题(至少三次的问题,到底有哪些脆弱性,理出来);OTP完整性攻击(篡改密文 from bob from eve );
-
RC4的缺陷(WEP);Salsa20的构造(很无聊,知道他是安全的;要知道哪些流密码是安全的哪些是不安全的;标准化的东西记住也没有用)
- 语义安全性:不会考太多,没有太多有关语义安全性的证明题;更多是分析以及找到一些攻击
- 证明的部分不用花太多时间,要理清楚他们之间的关系(比如流密码:随机生成器和消息异或,会出现什么样的攻击);攻击比较容易考(11:39)
- 太抽象了,不知道在说什么,感觉是要把各个密码的理论构造看懂
- 攻击多看
- 攻击比证明重要,哈哈
====分组密码
- DES为什么不安全?因为S盒有线性关系;DES使用feistel网络;AES没有用Feistel网络;
- 实现中出现的问题:侧信道,时间攻击,错误攻击
- 测信道攻击:包括计时攻击,针对功率的攻击,
- 错误攻击:对解密者返回的错误进行分析
- 线性分析不考,知道对对称密码来说,线性分析很简单,就可以对其进行破解
- 只要知道AES是安全的就好;AES和3DES相同的安全等级下,谁的效率更高:AES效率更高;3DES:加密一次解密一次再加密一次;效果不好
====分组密码的使用
【着重看CBC模式的加密,怎么做的】
- 使用模式的安全,哪些安全哪些不安全。
- CBC模式的加密:需要使用随机IV,如果IV不随机,会导致什么安全性后果,如果IV可预测会出现什么问题,TLS1.0版本的bug
- 可预测CBC,看上一个
=====MAC
- 消息认证码,有些上课提到过:消息认证码和数字签名的关系;
- 签名只有发送发可以加密,任何人都可以验证;MAC只有收方可以验证(可以同时确认来源以及防止篡改)
- MAC的定义,以及安全MAC的定义;存在性伪造的定义,CPA下的存在性伪造的定义;所有的伪造的方法以及伪造后怎么修复;存在性伪造会有一个简单的让你伪造的题目
- 着重看一下ECBC-MAC(encrypted CBC-MAC = CBC-MAC)会有什么问题
- 需要两个key
- 通过PRP定义一个新的PRF:

===hash
- hash和数字签名结合在一起考
- 生日攻击;以根号t的时间找到,hash至少要160以上;要了解一下这个(阈值??)
- 哪些hash安全哪些不安全

- SHA1 不安全,输入160bits 通用攻击2^80
- SHA256 安全 输入256bits 通用攻击2^128
- SHA512 安全,输入512bits 通用攻击2^256
- 量子计算机优化
===认证加密
-
padding oracle的攻击实验;以及它的原理
-
对于WEP不考(不考大题),要把TLS的注意一下,TLS要考大题;以及它的缺陷怎么修复
- TLS协议哈希函数:使用HAMC-SHA1-96
- TLS1.2 (TLS记录协议)【先计算MAC再加密】
- 有两个单向密钥k_{b to s} 和 k_{s to b} ;每个方向维护一个计数器ctr
- 加密 CBC-AES 128 HMAC-SHA1;E(k,data,ctr)
- 先算tag,再pad,再CBC加密,再接到header后

- 解密
- 先CBC解密,pad失败则发送失败;检查tag,检查失败则发送失败

- TLS 1.1漏洞
- CBC的IV是可预测的;下一个IV是本次记录的最后一个密文分块,不是CPA安全的
- 有padding oracle攻击:根据服务器返回的错误消息,可以得知密文的padding是否有效,(对不同的错误会返回不同的响应)
- 长度泄露:TLS头会泄露TLS记录的长度(也可以通过监听网络流量获取)
- 对TLS实现IMAP的padding oracle攻击
===密钥交换
===数论
===RSA
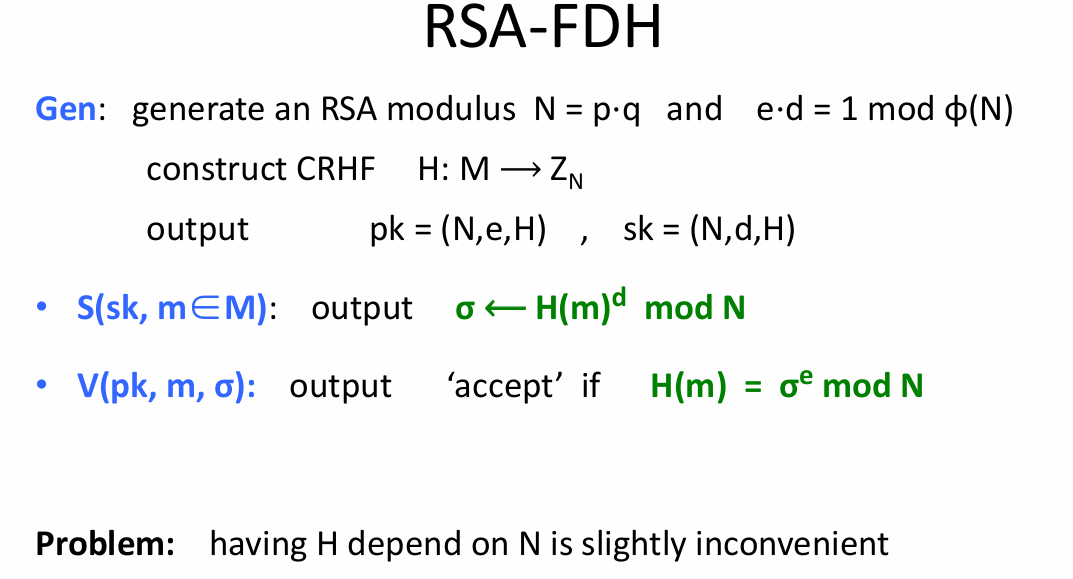
- RSA公钥加密怎么做
- textbook RSA是怎么做的;对教科书RSA的攻击(有点像中间相遇)
- 要会写RSA陷门(基本功)
- 要知道CPA安全性的定义(公钥安全的)
- 公钥加密的语义安全性(IND-CPA)
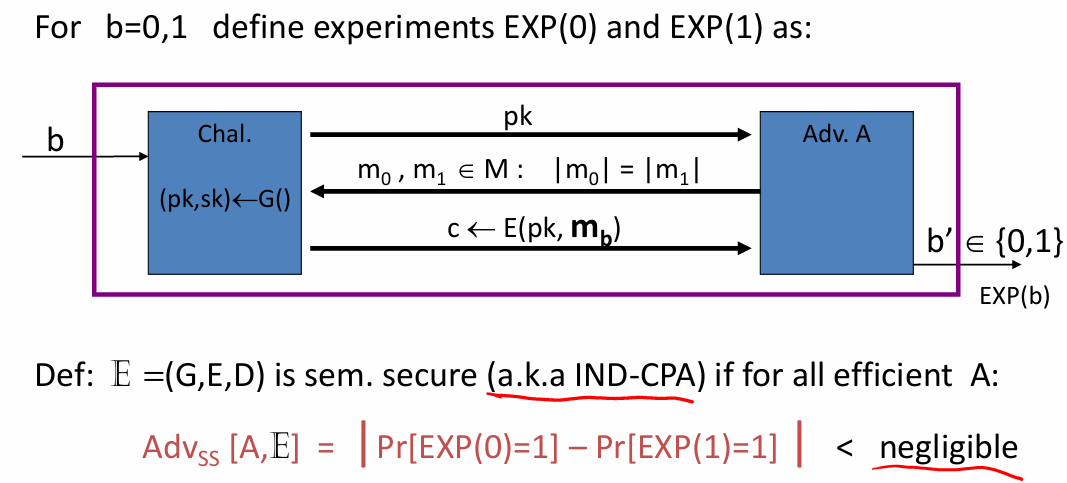
- 假如给你一个方案,你要会证明CPA安全性,可能需要规约;课本上会归约到困难问题,有时候也会归约到两个算法的问题;归约到陷门函数。
===Elgamal(自己加的 )
- 有一道大题有关ELGAMAL,和DH密钥协商类似;基于椭圆曲线
- 这是在说谜语吗,ELGAMAL到底要啥?只能把ppt 12-pubkey-dh-annotated全看一遍了