编码理论
知识体系
整数与多项式
- 辗转相除法: 最终
- 性质:
- 如果k是a,b的公因子,则k一定整除
- 最大公因子 一定存在整数
- 性质:
- 整数的同余和剩余类
- 同余:a,b有相同余数记作
- 剩余类:模d运算余数相同的元素构成的集合为剩余类,记作
- 模d的全体剩余类对模d假发和模d乘法满足封闭性
- 剩余类的加法和乘法运算: 、
- 多项式与不可约多项式
- 系数取自 的多项式可表示为
- 首一多项式:多项式最高次数系数是1的多项式
- 多项式的阶:多项式中系数不为0的x的最高次数
- 既约多项式/不可约多项式:阶大于0且在给定集合F上除了常数和常数与本身的乘积之外,不能被其它多项式除尽的多项式
- 一个多项式是否为不可约多项式,与系数所在的集合F有关( 在实数集合上不可约,在负数集合上可约,在 上可约)
- 多项式带余除法
- 给定两个多项式 且 一定存在唯一多项式 使得 记作
- 余元定理:如果 是 上的多项式, 则用一次多项式x-a除 所得元素一定是F中的元素 【F是数域,一次多项式做除法,余式一定小于一次,即常数】
- 余元定理推论【判断不可约多项式】:如果 是 中的多项式, 那么 是 的根当且仅当 整除
- 多项式同余和剩余类
- 同余 ,其中,
- 剩余类
- 剩余类的加法和乘法运算:
$$a(x){\oplus}b(x)=a(x)+b(x)$$
$$a(x){\otimes}b(x)=[a(x)b(x)] \bmod{p(x)}$$
加法群与乘法群
- 群的定义:集合+一种运算
- 封闭性
- 结合律
- 存在单位元e
- 对任何元素都有逆元
- 特殊群
- 交换群:群的运算满足交换律
- 群的阶:群中所含的元素的个数
- 有限群:阶是有限的
- 加法群:
- 对于任意正整数d,模d的所有剩余类集合 关于模d的加法构成加法交换群,阶为d,记作
- 对于任意多项式f(x),模f(x)的所有剩余类集合 关于模f(x)的加法构成加法交换群,阶为d,记作
- 乘法群:
- 若p为素数,则模p的所偶非零剩余类的集合为 ,其关于模p的乘法构成乘法交换群,阶为p-1 记为
- 若m为合数,则模m的所有非零剩余类的集合 关于模m的乘法无法构成群 (如 )
- 若 是 中的不可约多项式,则模 的所有非零剩余类 关于模 的乘法构成乘法交换群,记为
- 若 不是 中的不可约多项式,那么关于模 的乘法不构成群。
- 模p的乘法群:在p较小的时候可以通过直接计算得到,如果p较大时,则元素的逆元要通过辗转相除法得到
- 模 的乘法群
群、环、域
群
- 循环群:由元素 的一切幂次构成的群 (0次-n-1次)【对于加群,幂次就是一次加,乘就是一次乘】
- 循环群是交换群
- 元素的阶:使 的最小正整数n称为元素 的阶
- 性质:
- 如果a是n阶元素,那么 的充要条件是n整除m
- 某一个群中,a是n阶元素,b是m阶元素,且(n,m)=1则元素ab的阶为nm
- 若a是n阶元素,则 的阶为 n/(n,k)
- 性质:
- 生成元:如果 的阶等于循环群 G 的阶,则 称为G的生成元
- 子群:如果群G的非空子集G’对于群G中所定义的代数运算也构成群,则G’称为G的子群【子群、运算相等】
- 交换群 的任意元素都能生成一个循环子群, ,元素 的阶就是循环子群 的阶
- 有限群的子群的阶一定整除群的阶
- 陪集:G’是G的非空子群,取 则称 为G’ 的左陪集, 为G’的右陪集;如果G为交换群,那么左右陪集相等
- 如果G’的阶为n,且G’为G的子集,如果G的阶为n*m,则可以将G完备地分成m个陪集(子群本身也是一个陪集)【应用:整理的第七题】
- 几点说明:
- 陪集首如果是G’中的元素,则陪集h*G’与子群G’相同
- 陪集首不是h的元素,则h*G’与G’的交为空集
- 陪集首 如果不是陪集 中的元素,则两陪集 与 相交为空集【陪集首可以确定陪集】
- 陪集 中的每个元素都可以作为其陪集首,陪集元素不变,仅排列顺序改变
环
- 环的定义:集合+加法+乘法
- F对加法是一个交换群
- F对乘法具有封闭性、结合律
- 乘法对加法满足分配律:a(b+c)=ab+ac (a+b)c=ac+bc
- 如果乘法满足交换律,则这个环叫做交换环
- 环的性质:
- 环中可以有零因子
- 有单位元且每个非零元素都有逆元且非可换的环叫做除环
- 子环:是子集且加法和乘法运算也构成环
- 剩余类环
- 以整数m为模的除法得到的全体剩余类可以构成环,称作整数剩余类环
- 模f(x) 的全体余式对模f(x)的运算构成交换环,称作多项式剩余类环
域
- 域的定义:集合+加法+乘法
- 对加法构成交换加群
- 非零元素全体对乘法构成交换乘群
- 乘法对加法具有分配律 a(b+c)=ab+ac (a+b)c=ac+bc
- 域是一个可交换的、有单位元的、非零元素有逆元的环
- 和环相比,对乘法多了交换群的定义
- 无限域和有限域
- 无限域:元素个数无限的域
- 有限域:元素个数有限的域 GF(q)表示q阶有限域
- 有限域的例子:二元域 ,p元域
- 有限域的构造:
- 整数有限域:如果p是素数,那么以p为模的全体整数剩余类构成阶为p的有限域, 记为 ,或者
- 多项式: 如果f(x)是F[x]上的n次不可约多项式,则F[x]关于模f(x)的全体剩余类的集合记为 关于模f(x)的加法和乘法构成域,记为
- 有限域的阶:如果F是q个元素的有限域,f(x)的次数为n,则 为 个元素的有限域
- n=1时, 即F (x是一次,则剩余类就是0次)
- F是 的子域
- 有限域的结构
- 任意素数p都有p个元素的有限域;对任意正整数n,在 一定存在n次不可约多项式f(x)
- 一定存在 个元素的有限域,即 注意这是多项式有限域,记为
- 任意有限域元素的个数一定是 p为素数,n为正整数
- 有限域的特征(加法结构)
- 特征是指:m个1的和为0,则m就是该域的特征,如果对任意正整数m,和都不为0,则域的特征为0
- 无限域的特征为0
- 有限域 的特征为p;特征为p的有限域一定可以记为
- 特征为p的有限域 中,对任意两个元素 $\alpha \beta $ 一定有
- 特征是指:m个1的和为0,则m就是该域的特征,如果对任意正整数m,和都不为0,则域的特征为0
- 有限域的本原元
- 本原元:有限域 GF(p) 中,如果某一元素 的阶【关于乘法的阶】为 p-1 则称 为该域中的本原元
- 阶是指n次方为e,乘法e是1[因为是关于乘法]
- p-1 乘法去除0元素
- 本原元:有限域 GF(p) 中,如果某一元素 的阶【关于乘法的阶】为 p-1 则称 为该域中的本原元
有限域
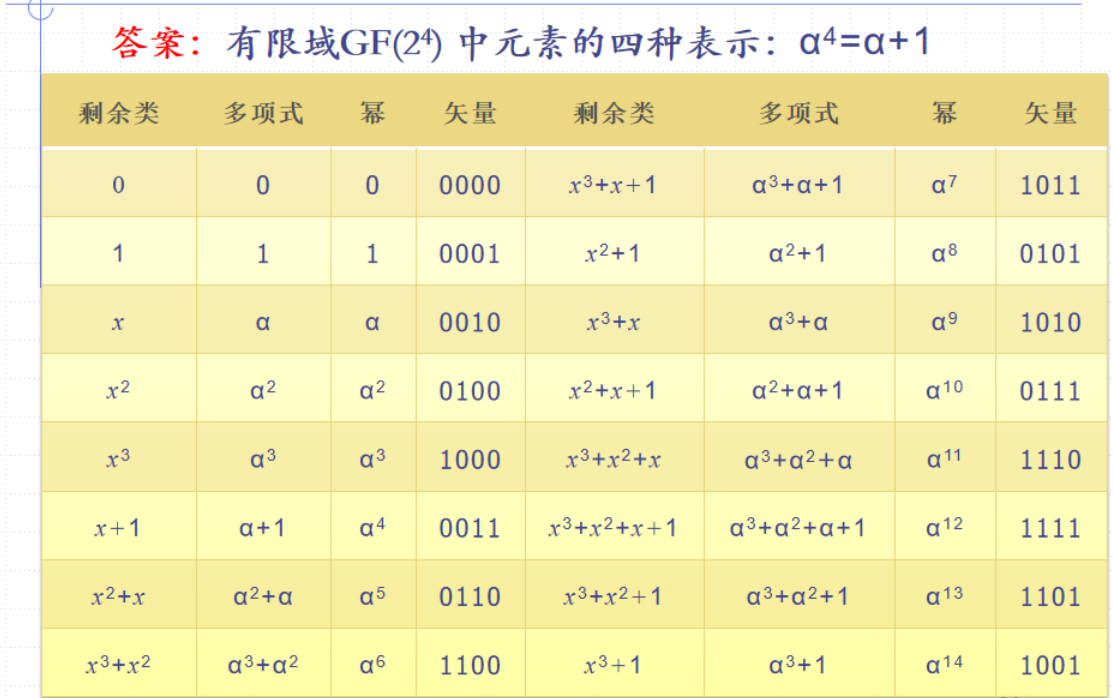
- 有限域的剩余类表示
- 可以看作 以三次不可约多项式 为模的全体剩余类的集合;以剩余类表示,加法易求,乘法不易求
- 有限域的幂表示
- 四种表示法:剩余类、多项式(x换成 )、幂、矢量表示
- 有限域中的元素
- 有限域GF(q)中的所有元素都是方程 的根,反之,方程 的根必在 GF(q)中
- 有限域 中任意元素 均有
- 有限域GF(q)中的所有元素都是方程 的根,反之,方程 的根必在 GF(q)中
- 共轭根组
- 如果f(x)是系数取自GF(p)的k次不可约多项式, 若 是f(x)的根,则 也是f(x)的根
- 称 为f(x)的共轭根组
- 最小多项式
- 系数取自GF(p),以 为根的所有首一多项式中,必有一个次数最低的多项式,称为 的最小多项式
- 该最小多项式在GF(p)上不可约
- 任意 的最小多项式是唯一的
- 的最小多项式整除任何以 为根的多项式(包括 )
- 系数取自GF(p),以 为根的所有首一多项式中,必有一个次数最低的多项式,称为 的最小多项式
- 既约多项式/不可约多项式:
- GF(2)上的m次多项式不能被GF(2)上任何次数小于m但是大于0的多项式整除,则称其为GF(2)上的既约多项式
- 在GF(2)上,如果f(x)有偶数项,则能被x+1整除,不是既约多项式
- 在GF(2)上,如果f(x)没有常数项,则能被x整除,不是既约多项式
- GF(2)上任意m次既约多项式整除
- 2次不可约多项式整除 x^3+1
- 三次不可约多项式整除 x^7+1
- 对任意正整数m,存在m次不可约多项式
- GF(2)上的m次多项式不能被GF(2)上任何次数小于m但是大于0的多项式整除,则称其为GF(2)上的既约多项式
- 本原元多项式:如果m次不可约多项式p(x)能整除 的最小正整数n满足 n=2^m-1 则称p(x)为本原多项式
- 即判断能不能整除
- 本原多项式性质
- 本原多项式一定是不可约多项式,不可约多项式不一定是本原多项式
- 给定正整数m,m次本原多项式不唯一,可以查表得到
纠错编码的基本概念
- 信源编码:目的是压缩冗余度,提高信息压缩率;
- 信道编码:目的是提高信息传输时的抗干扰能力,增加信息传输的可靠性
- 纠错编码是信道编码,具有抗干扰能力
- 消息集合: 消息的长度为5,消息中每个值都在
- 编码:低维空间到高维空间,通过一个映射 将其映射到编码空间
- 码: ;
- 码字: 中的向量
- 码元:码元是码字的分量
- 字: 中的向量
- q元码:码字中每个分量在 种取值的码,二元码是在 种取值的码
- 信息率: k/n(对于F2来说);对于Fn:
- 检错编码:能够判断错误有没有发出
- 纠错编码:能够正确译出发送方发送的码字
- 极大似然译码
- 检错、纠错能力判定
线性分组码
编码问题
- 线性分组码的定义:如果C是码长为n的q元码,即 ,若C是 子空间,称C为码长为n的q元线性分组码
- 子空间满足:v1+v2仍属于C
- 子空间满足:cv属于C
- 子空间满足:向量的线性组合还在C中
- 如果C是 的k维子空间,则 【映射后的消息编码和消息空间同构】;存在一一映射使得 :从
- 生成矩阵:存在一组基生成C,由基向量构成的矩阵记为G,称为生成矩阵【生成矩阵:列:空间的维数,行:C中向量的个数】
- C中任一码字是G中行向量的线性组合,即由G生成
- G中行向量的所有线性组合都是码字,即属于C
- 生成矩阵是否是唯一的?不是唯一的,C是 的子空间,G是C的一组基向量构成的矩阵,基向量不唯一,则矩阵不唯一
- 生成矩阵中的基向量都是线性无关的,如何判断一组向量线性无关?看前n位是否为单位矩阵
- 线性分组码由生成矩阵唯一确定
- 同一线性分组码的生成矩阵不唯一
- 同一线性分组码C的不同生成矩阵确定的C集合是唯一的
- 不同生成矩阵下,统一原始消息对应的码字可能不同
- 同一线性码C的生成矩阵之间是什么关系?
- 他们是行等价的,即存在可逆矩阵P,使得G1=PG2
- 如果A是域F上的一个m*n矩阵,则A一定行等价与一个阶梯矩阵
- 系统码与等价的码
译码问题
- 对偶子空间
- 如果W是 的一个子空间,令 , 是W的对偶子空间
- 对偶子空间是相互的
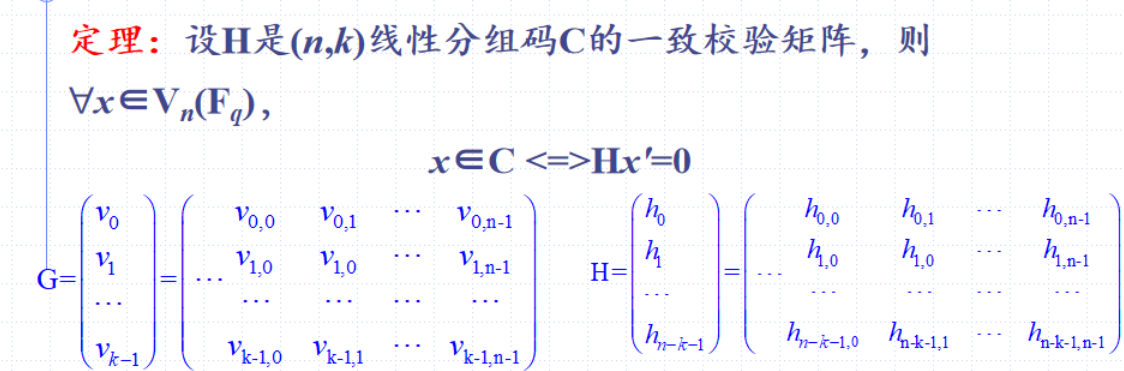
- 一致校验矩阵
- 校验子
- H是C的一致校验矩阵,任意x属于 则称Hx’为校验子
- 如果收到的字为r,则可以通过Hr’判断与r有相同校验子的字中找hamming距离最小的
- 使用C将 划分为多个陪集,由于 因此共有 个陪集====译码表
- 定理:任意 $x,y \in V_nF(q), $,则 的同一个陪集当且仅当
- 应用:如果e为Hr’的陪集首,如果收到r,则计算Hr’,如果Hr’=0,则译为r,如果Hr’不为0,则找Hr’为标记的陪集,陪集首为e,则将r译为r-e
- 译码表
1
2
3
4
51. C排在首行,0向量排在首位
2. 每一个陪集排成一行,共q^{n-k}行
a. 以校验子作为该行标记
b. 重量最小的向量排在该行首位,即0向量的下面
c. c+e排在码字c的下方- 如果陪集首不唯一,可以任选其一,此时为非确定译码
- 译码表满足极大似然法则,因为Hamming(r,r-e)<Hamming(r,a) (a属于C,a不为r-e)
- 证明:
- 证明:
- 何时正确译码
- 译码表中陪集首与校验子的求法:
- 选取重量为1的向量作为陪集首(只有1个为1的向量)
- 若重量为1的向量不够(不够q{k-1}),则取重量为2的向量计算校验子,知道获得q{k-1}个校验子为止
- 译码问题:
- 发a,收r;
- 首先计算r的校验子Hr’
- 找到Hr’对应的陪集首e
- 将r译为r-e
- 发a,收r;
考点整理
- 辗转相除法求最大公因子,并将最大公因子表示成两个数的线性组合
- 步骤:
1
2
31. 辗转相除法求
2. 表示为r=a-qb的形式
3. 从最大公因子的式子反推,不断将上一个结果替代
- 判断一个多项式是否为不可约多项式,以及对应的多项式【注意四次多项式】
- 注意:如果是二次/三次多项式,则可以直接通过一次因式判断;如果是4次多项式,则要判断一次因式【余元定理】和二次因式【手算?】

- 考试第一个大题:求多项式最高公因式,并将其表示为线性组合【多项式辗转相除法】

- (不是考点,但是自己整理)全体剩余类求法: 以p(x)为模,最高次数不超过 的多项式集合,设p(x)最高次数为p, 表示 的系数 即 如果F是 那么只取0,1即可,如果是 则要取0,1,2
- 模 乘法群中元素 的逆元:考填空;如果简单,可以依次验证;如果复杂,则需要用辗转相除法
- 步骤:
1
2
3
4
5求p(x) 中f(x)的逆元
1. 辗转相除法求(p(x),f(x))
2. 将最大公因子1用p(x)和f(x)的线性组合表示
3. 将p(x)和f(x)的线性组合模p(x)
4. 模结果为B(x)f(x),则B(x)为f(x)的逆元
- 考试大题: 1.给定多项式,判断哪个是不可约多项式。2.模那个不可约多项式,构成乘法群,求逆元
- 步骤:
1
2
31. 判断不可约多项式:余元定理或者死算,注意1,2,3次判断1次即可;以上的要考虑不止一次
2. 模加和模乘运算
3. 求逆元(上一题的步骤;辗转相除法)

- (自己整理) 将群分为陪集的并
1
依次找群中的元素与集合进行运算,如果重复则跳过,每次都选择前面未出现的元素作为当前陪集的陪集首
- 写出所有子群
- 通常:<生成元>=G 其它的真子群按照实际写
- 判断是否为域:
1
2
31.先判断是否为群:满足封闭、结合、有单位元和逆元
2.判断是否为环:加法交换群,乘法满足封闭、结合律;乘法对加法满足分配律
3.判断是否为域:乘法是不是交换群- 一些记号: x通常是一个无理数,表示
- 比如: 是域,且是无限域; 不是域,因为 没有逆元
- 判断是否有N个元素的有限域:判断依据:N是不是等于p的n次方,注意p为任意素数。则对应的有限域为 ,其中,f(x)是n次不可约多项式
- 如有8个元素的有限域: 其中f(x)是一个3次不可约多项式
- 有8 9 23个元素的有限域,但是没有35个元素的有限域
- 求本原元
- 如,求GF(7)的本原元是多少:直接求
- 如,问某个元素是不是本原元
- 求f(x)共轭根组
1
2
3
40.先给句f(x),代入根,求beta的m次和beta的关系
1.看清域,看清p和k,其中,k是f(x)的次数(也是模f(x)构成的有限域 GF(p^m)的m)
2.求出根的p次方、p^2 次方直到根的p^(k-1)次方
3.将f(x)以根的次方表示
- 有限域的因式分解
一般题目会在系数域GF(p)上以不可约多项式f(x)构成有限域,求多项式在系数域上的分解g(x)结果[如果g(x)的次数为k]- 写出有限域 的特征
- 找本原元,并且写出有限域的元素的4种表示,在有限域(不可约多项式为模构成的) 上分解多项式
【分解结果一般是: 】 - 找出各个共轭根组,并构成相应最小多项式【最小多项式下标以共轭根组种元素的最低幂次表示】
- 化简最小多项式(利用f(x)化出来的幂次关系)
- 最小多项式的化简:
- 先展开式子,合并每个x的系数
- 化简系数:利用 对应的矢量的加法,得到的新矢量在表中寻找对应的
- 常数系数一般都是1
- 最小多项式的化简:
- 化简所有的最小多项式后(化简后的多项式没有 ),分解多项式,在有限域(不可约多项式为模构成的)上分解多项式的结果,组合称为多个最小多项式,最后使用最小多项式化简得结果替代。
- 找出所有的本原元和本原多项式
- 本原元找法:由于 是本原元,阶为 则利用 的阶为 算出其它元素的阶
- 本原多项式:本原元对应的多项式
- 简单说出一种判断线性码的纠错、检错能力的方法,并说出衡量其检、纠错能力的值
- 设C为码长为n的一个码:
- 若任意两个码字距离 t+1 则C是可检出t个差错的检错码
- 若确有两个码字的距离=t+1,则C不能检出t+1个差错
- 若任意两个码字的距离 2t+1,则C是可纠正t个差错的纠错码
- 若确有两个码字的距离=2t+1,则C不能纠正t+1个差错
- 通过码C的极小距离来衡量检错、纠错能力,极小距离是码C的两两码字的距离的最小值

- 设C为码长为n的一个码:
- 根据线性码的生成矩阵求出C
- 根据生成矩阵求出所有的消息,将消息映射成码字
- 画一个阶梯形矩阵并求出秩
- 只需要行初等变换,从上到下变,下面的不换到上面来
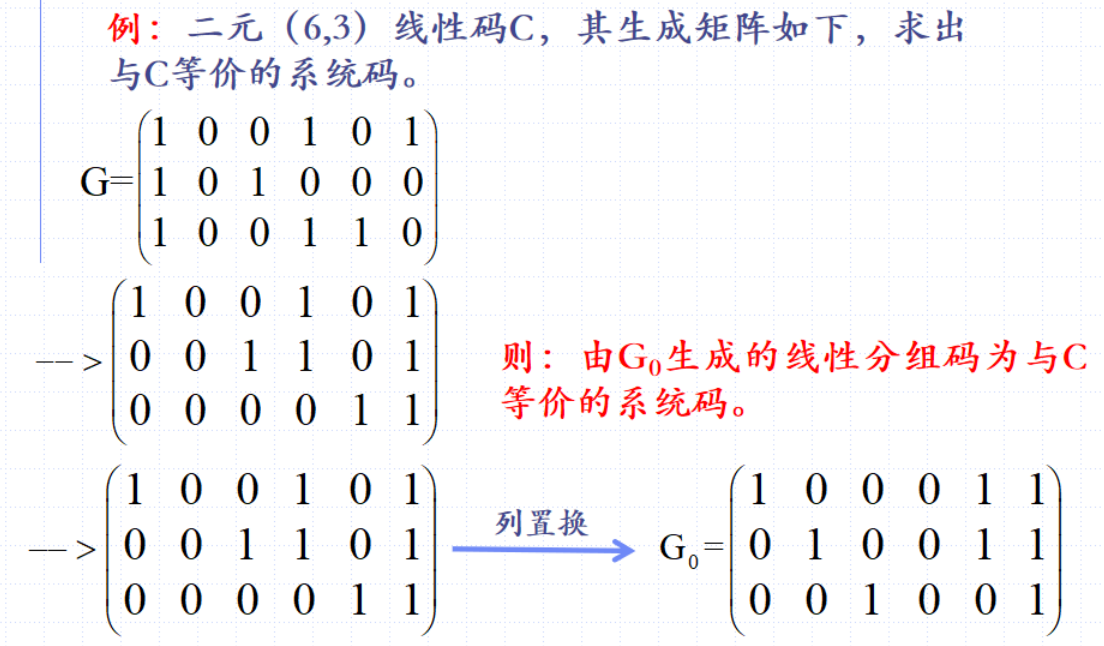
- 根据生成矩阵求出系统码
- 会判断线性分组码
- 已知G矩阵的维度,求H的维度
- G是 矩阵,H是 矩阵
- 求以G为生成矩阵的线性分组码的一致校验矩阵H====求域上齐次线性方程组Gx’=0的解空间的秩和解空间的一组基
- 求出H的维度
- 由生成矩阵G求一致校验矩阵H,即求Gx’=0的解空间的一组基
1
2
3
41. 首先 行初等变换,将G变化为阶梯型矩阵 G0
2. 解方程 G0x'=0
选出列中只有一个1的列,剩余的列是自由向量
对于自由向量,分别取1,如(1,0,0) (0,1,0) (0,0,1) - 线性分组码的译码问题【ppt例题】
- 线性分组码的检错能力和纠错能力
- C是线性码,C的极小重量等于C的极小距离,
- 定理1:设C为码长为n的线性码,若C的极小重量为t+1,则C是可以检出t个差错的检错码,是可以纠正 差错的纠错码
- 定理1’:不需要求极小重量,根据一致校验矩阵判断
C是q元(n,k)线性码,H是它的一个一致校验矩阵,如果H的任意t列都线性无关,有t+1列线性相关,则C的极小重量等于t+1,C是可以检t错的检错码,可以纠 错的纠错码 - 判断线性无关:先判断任意1列,再任意2列
编码理论
https://mapllle.site/2024/03/21/StudySHUSHU/CodingTheory/